Теория категорий
Теория категорий - раздел математики, изучающий свойства отношений между математическими структурами, независимо от внутреннего строения структур; абстрагируется от множеств и функций к диаграммам, где объекты связаны морфизм (стрелками). Теория категорий занимает центральное место в современной математике, она также нашла применение в информатике и в теоретической физике. Современное преподавание алгебраической геометрии и гомологической алгебры базируется на теории категории. Понятия теории категорий используются в языке функционального программирования Haskell.
ИсторияПонятие категория была введена в 1945 году. Своим происхождением и первичными стимулами развития теория категорий обязана алгебраической топологии. Дальнейшие исследования выявили объединяющую и унифицируя роль понятия категория и связанного с ним понятия функтора для многих разделов математики. Теоретико-категорний анализ основ теории гомологии привел к выделению в середине 50-х гг 20 в. так называемых абелевых категорий, в рамках которых оказалось возможным осуществить основные построения гомологической алгебры. В 60-е гг 20 в. определился растущий интерес к неабелевих категорий, вызванный задачами логики, общей алгебры, топологии и алгебраической геометрии. Интенсивное развитие универсальной алгебре и аксиоматическое построение теории гомотопий положили начало различным направлениям исследований: категорному изучению многообразий универсальной алгебре, теории изоморфизме прямых разложений, теории связанных функторов и теории двойственности функторов. Дальнейшее развитие обнаружил существенный взаимосвязь между этими исследованиями. Благодаря возникновению теории относительных категорий, широко использует технику связанных функторов и замкнутых категорий, была установлена двойственность между теорией гомотопий и теории универсальных алгебр, основанная на интерпретации категорних определений моноида и комоноида в соответствующих функторов. Другой способ введения дополнительных структур в категориях связан с заданием в категориях топологии и построении категории пучков над топологической категории (так наз. топосы ).
ОпределениеКатегорияКатегория
Примеры категорий
Все вышеперечисленные категории допускают изоморфное вложение в категорию множеств. Категории, с таким свойством, называются конкретными. Не всякая категория является конкретной, например категория, объектами которой являются все топологические пространства, а морфизм - классы гомотопных отображений. Коммутативные диаграммыСтандартным способом описания утверждений теории категорий является коммутативные диаграммы. Коммутативна диаграмма - это ориентированный граф, в вершинах которого находятся объекты, а стрелками есть морфизм или функторы, причем результат композиции стрелок не зависит от выбранного пути. Например, аксиомы теории категорий можно записать с помощью диаграмм:
Категория с объектами X, Y, Z и морфизм f, g. ДвойственностьДля категории
Вообще, для любого утверждения теории категорий можно сформулировать двойственное утверждение с помощью обращения стрелок.Часто двойное явление обозначается тем же термином с приставкой ко- (см. примеры ниже). Справедлив так принцип двойственности: утверждение г истинно в теории категорий тогда и только тогда, когда в этой теории истинно двойственное утверждение г *. Многие понятия и результатов в математике оказались двойственным друг другу с точки зрения понятий теории категорий: иньективнисть и сюрьективнисть, многообразия и радикалы в алгебре и т.д. Изоморфизм, эндоморфизм, автоморфизмыМорфизм Морфизм, в которых начало и конец совпадают, называют эндоморфизмамы. Множество ендоморфизмив Эндоморфизмы, которые одновременно являются изоморфизм, называются автоморфизмом. Автоморфизмы любого объекта образуют группу автоморфизмов Мономорфизм, эпиморфизм, биморфизмМономорфизм - это морфизм Эпиморфизм - это такой морфизм, что для любых Биморфизм - это морфизм, являющийся одновременно мономорфизм и эпиморфизмом. Любой изоморфизм является биморфизмом, но не любой биморфизм является изоморфизмом. Мономорфизм, эпиморфизм и биморфизм являются обобщениями соответственно. Любой изоморфизм есть мономорфизм и эпиморфизмом, обратное, вообще говоря, верно не для всех категорий. Инициальный и терминальный объектыИнициальный (начальный, универсально отталкивающий) объект категории - это такой объект, с которого существует единственный морфизм в любой другой объект. Если инициальные объекты в категории существуют, то все они изоморфны. Двойственным образом определяется терминальный объект - это такой объект, в который существует единственный морфизм из любого другого объекта.
Произведение и сумма объектовПроизведение объектов A и B - это объект Дуально определяется прямая сумма или кодобуток A + B объектов A и B. Соответствующие морфизм Если произведение и кодобуток существуют, то они определяются однозначно с точностью до изоморфизма.
|
|
Решение методом Гаусса | Система уравнений методом Гаусса Элементарные преобразования матриц Вернуться в оглавление: Высшая математика |

 состоит из класса
состоит из класса  , элементы которого называются объектами категории, и класса, элементы которого называются морфизм категории. Эти классы должны удовлетворять следующим условиям:
, элементы которого называются объектами категории, и класса, элементы которого называются морфизм категории. Эти классы должны удовлетворять следующим условиям: ; если, то А называется началом, или областью определения морфизму f, а В - конец, или область значений f.
; если, то А называется началом, или областью определения морфизму f, а В - конец, или область значений f. задан частичный закон умножения: произведение морфизм
задан частичный закон умножения: произведение морфизм  и
и  определены тогда и только тогда, когда В = С, и принадлежит классу
определены тогда и только тогда, когда В = С, и принадлежит классу  для любых морфизм для которых данные произведения определены.
для любых морфизм для которых данные произведения определены.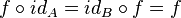 для
для 
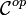 , в которой:
, в которой:
 и. Два объекта, между которыми существует изоморфизм, называются изоморфными. В частности, тождественный морфизм является изоморфизмом, поэтому любой объект изоморфен сам себе.
и. Два объекта, между которыми существует изоморфизм, называются изоморфными. В частности, тождественный морфизм является изоморфизмом, поэтому любой объект изоморфен сам себе.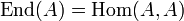 является моноидом относительно операции композиции с единичным элементом.
является моноидом относительно операции композиции с единичным элементом. по композиции.
по композиции. из
из  следует, что. Композиция мономорфизм является мономорфизм.
следует, что. Композиция мономорфизм является мономорфизм.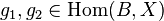 из
из  следующего.
следующего.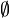 , терминальным - множество из одного элемента.
, терминальным - множество из одного элемента. с морфизм
с морфизм 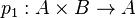 и
и  такими, что для любого объекта
такими, что для любого объекта  и
и 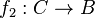 существует единственный морфизм
существует единственный морфизм 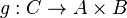 такой, что. Морфизм
такой, что. Морфизм  и
и 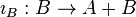 называются вложениями. Несмотря на свое название, в общем случае они могут и не быть мономорфизм.
называются вложениями. Несмотря на свое название, в общем случае они могут и не быть мономорфизм.








