CПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ
(Способ вращения без указания оси поворота) Из планиметрии известно о преобразованиях “движение”, которые включают в себя ряд преобразований: параллельный перенос, вращение, преобразование симметрии и гомотетию. При этом одни преобразования могут быть заменены другими. Например, в случае параллельного переноса, а затем вращения отрезка, оба преобразования могут быть сведены к одному повороту, центр О вращения при этом может быть найден (рис.5.15, 5.16).
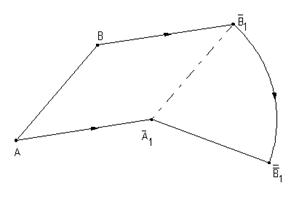
Рис.6.15(Параллельный перенос) Рис.6.16 (Поворот) Плоскопараллельный перенос фигуры в пространстве параллельно плоскости проекций, хотя и меняет положение фигуры, проекция этой фигуры на соответствующую плоскость проекций остается конгруэнтной. Рассмотрим способ плоскопараллельного переноса на примере решения четырех основных задач на преобразование комплексного чертежа. 1-я и 2-я основные задачи (рис.6.17), 3-я и 4-я основные задачи (рис.6.18). Последовательность преобразования ясна из чертежей.
Рис.6.17 Рис.6.18 |