ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ

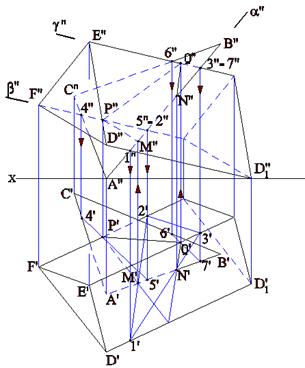
Задача на пересечение многогранника плоскостью общего положения решается с помощью вспомогательных секущих плоскостей. На рис. 4. 12а приведен пример пересечения трехгранной призмы DEFD₁E₁F₁ плоскостью треугольника АВС.

Рис. 4.12а

Задача на рис. 4. 12а решена с помощью вспомогательных секущих плоскостей:

a(a``), проведенной через сторону АВ треугольника АВС, которая пересекла призму по треугольнику 123, точки пересечения M и N c FD принадлежат искомой линии пересечения,

и вспомогательных секущих плоскостей b(b`) и g(g``), с помощью которых найдены соответственно точки P и Q линии MPQN пересечения призмы DEFD₁E₁F₁ c треугольником АВС.

Определение видимости на чертеже не показано.

ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ К ПЛОСКОСТЯМ ПРОЕКЦИЙ

ВЗАИМНАЯ ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ

НЕКОТОРЫЕ СВОЙСТВА ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ

ПОВЕРХНОСТИ ВРАЩЕНИЯ

Вернуться в оглавление: НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ