|
1) Сравнительный анализ Ряды динамики, изучающие изменение статистического показателя, могут охватывать значительный период времени, на протяжении которого могут происходить события, нарушающие сопоставимость отдельных уровней ряда динамики (изменение методологии учета, изменение цен и т.д.). Для того, чтобы анализ ряда был объективен, необходимо учитывать события, приводящие к несопоставимости уровней ряда и использовать приемы обработки рядов для приведения их в сопоставимый вид: - смыкание рядов динамики – применяется, когда уровни рядов динамики несопоставимы в связи с территориальными, ведомственными, организационными и изменениями в методологии исчисления показателей. Осуществляется 2 способами:
- по данным двух рядов определяется коэффициент соотношения уровней переходного периода (момента), т.е. периода, в котором произошло изменение, а уровни, предшествующие переходному периоду, умножаются на этот коэффициент и получаются условно сопоставимые уровни и ряды смыкаются;
- уровни переходного периода принимаются для каждого из смыкаемых рядов за 100%, а остальные рассчитываются в процентном соотношении к этому уровню.
- Приведение рядов динамики к общему основанию – используется для рядов динамики различных явлений при разных единицах измерения и т.п. Чтобы привести ряды динамики к единому основанию, необходимо уровни рядов сравнить с одним уровнем, принятым за базу.
2) выявление основной тенденции в рядах динамики
Наиболее важна при анализе ряда динамики его основная тенденция развития, но часто по одному лишь внешнему виду ряда динамики ее установить невозможно, поэтому используют специальные методы обработки, позволяющие показать основную тенденцию ряда: - метод укрупнения интервалов - суть метода в том, чтобы от интервалов, или периодов времени, для которых определены исходные уровни ряда динамики, перейти к более продолжительным периодам времени и посмотреть, как уровни ряда изменяются в этом случае;
- метод скользящих средних. Суть метода заключается в том, что фактические уровни ряда заменяются средними уровнями, вычисленными по определённому правилу. Сглаживание методом скользящих средних можно производить по трем, четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней. Метод скользящих средних не позволяет получить численные оценки для выражения основной тенденции в ряду динамики, давая лишь наглядное графическое представление;
- Метод аналитического выравнивания - наиболее совершенным способ определения тенденции развития в ряду динамики. При этом методе исходные уровни ряда динамики
 заменяются теоретическими или расчетными заменяются теоретическими или расчетными  , которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др. , которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др. Подбор подходящей функциональной зависимости должен опираться на теоретический анализ сущности изучаемого явления и на данные, полученные в результате применения других способов выравнивания. Этот метод вызван необходимостью прогнозирования. Самая простая зависимость – линейная.
 , ,
где  - коэффициенты, определяемые в методе аналитического выравнивания; - коэффициенты, определяемые в методе аналитического выравнивания;
 - показатель времени - показатель времени
Расчет коэффициентов 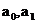 ведется на основе метода наименьших квадратов: прямая, выравнивающая ряд, должна проходить в максимальной близости от фактических уровней ряда (сумма квадратов отклонений фактических значений от теоретических уровней ряда должна быть наименьшей). ведется на основе метода наименьших квадратов: прямая, выравнивающая ряд, должна проходить в максимальной близости от фактических уровней ряда (сумма квадратов отклонений фактических значений от теоретических уровней ряда должна быть наименьшей). Для применения этого способа применяют систему двух уравнений: Если вместо абсолютного времени 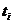 выбрать условное время таким образом, чтобы выбрать условное время таким образом, чтобы  , то , то 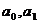 находятся: находятся:
 
Затем составляется новый выровненный ряд и делаются прогнозы:
- экстраполяция – определение уровней последующих периодов;
- интерполяция – определение уровней промежуточных периодов.
|











