Кафедра САУ
В.П. Литвинов
Однофазные электрические цепи
синусоидального тока
Задание на типовой расчет
Красноярск, 2012
Содержание работы
I. Для указанной схемы при наличии взаимной индуктивности:
1. Найти токи во всех ветвях электрической схемы.
2. Составить баланс активных и реактивных мощностей.
3. Построить топографическую диаграмму токов и напряжений цепи.
4. Построить волновую диаграмму токов и напряжения для ветви, содержащей источник электрической энергии.
II. Для указанной схемы произвести развязку взаимной индуктивности и методом пропорционального пересчета:
1. Найти токи во всех ветвях электрической схемы.
2. Составить баланс активных и реактивных мощностей.
III. Для указанной схемы при присутствии взаимной индуктивности методом сигнальных графов найти ток через источник (по заданию преподавателя).
Указания
1. Сопротивления взаимных индуктивностей находятся из выражения
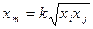 , где
, где 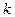 - коэффициент индуктивной связи.
- коэффициент индуктивной связи.
2. На топографических диаграммах должны быть показаны векторы напряжений на всех элементах схемы.
3. Напряжения на элементах схемы, обладающих взаимной индуктивностью, должны быть разделены на составляющие.
Числовые данные параметров схем
Таблица 1
| № п/п | 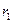
| 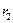
| 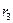
| 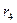
| 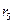
| 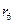
| 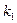
| 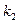
| 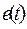
|
| Ом | Ом | Ом | Ом | Ом | Ом | В | |||
| 0,5 | 0,5 | 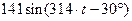
| |||||||
| 0,2 | 0,8 | 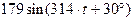
| |||||||
| 0,4 | 0,6 | 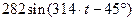
| |||||||
| 0,6 | 0,4 | 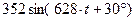
| |||||||
| 0,8 | 0,2 | 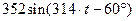
| |||||||
| 0,3 | 0,3 | 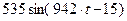
| |||||||
| 0,5 | 0,3 | 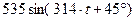
| |||||||
| 0,8 | 0,8 | 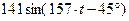
| |||||||
| 0,6 | 0,2 | 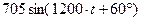
|
Таблица 2
| № п/п | 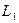
| 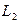
| 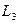
| 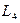
| 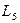
| 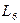
| 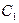
| 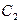
| 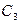
| 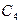
| 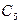
| 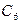
|
| Гн | Гн | Гн | Гн | Гн | Гн | мкФ | мкФ | мкФ | мкФ | мкФ | мкФ | |
| 0,02 | 0,03 | 0,04 | 0,015 | 0,035 | 0,06 | |||||||
| 0,04 | 0,02 | 0,03 | 0,01 | 0,05 | 0,05 | |||||||
| 0,03 | 0,06 | 0,04 | 0,02 | 0,05 | 0,04 | |||||||
| 0,05 | 0,04 | 0,05 | 0,025 | 0,02 | 0,03 | |||||||
| 0,03 | 0,05 | 0,06 | 0,04 | 0,04 | 0,02 | |||||||
| 0,05 | 0,04 | 0,02 | 0,03 | 0,035 | 0,06 | |||||||
| 0,04 | 0,03 | 0,035 | 0,04 | 0,03 | 0,045 | |||||||
| 0,06 | 0,06 | 0,05 | 0,05 | 0,08 | 0,03 | |||||||
| 0,04 | 0,02 | 0,06 | 0,03 | 0,05 | 0,025 |
Типовой расчет
Цепь синусоидального тока
Цель расчета: освоение символического метода расчета целей синусоидального тока при наличии индуктивных связей, построение векторных диаграмм токов и топографических диаграмм напряжений заданной цепи, применение основных положений теории к расчету конкретной электрической цепи переменного тока.
Исходные данные: схема электрической цепи и ее параметры.
Содержание работы: приведено в задании на типовой расчет.
Литература
Атабеков Г.И., Теоретические основы электротехники, ч.1, М, энергия, 1970, Индуктивно-связанные электрические цепи, стр. 216-231.
Бессонов Л.А., Теоретические основы электротехники, М, Высшая школа, 2003.
Пример выполнения расчета
В качестве примера приведем расчет электрической цепи, схема которой показана на рис. 1.
 |
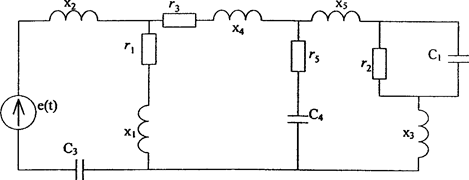
Рис. 1. Схема электрической цепи.
Параметры элементов цепи:
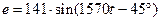 В;
В;
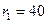 Ом;
Ом; 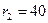 Ом;
Ом; 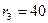 Ом;
Ом; 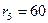 Ом;
Ом;
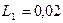 Г;
Г; 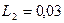 Г;
Г; 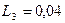 Г;
Г; 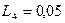 Г;
Г; 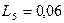 Г;
Г;
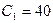 мкФ;
мкФ; 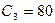 мкФ;
мкФ; 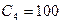 мкФ;
мкФ;
Коэффициенты индуктивной связи 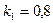 ;
; 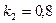 .
.
1. Нахождение токов в ветвях электрической схемы.
1.а) Определяем сопротивления элементов электрической цепи.
Сопротивления индуктивные:
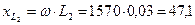 Ом;
Ом; 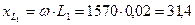 Ом;
Ом;
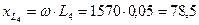 Ом;
Ом; 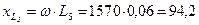 Ом;
Ом;
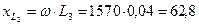 Ом;
Ом;
Сопротивления емкостные:
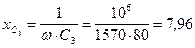 Ом;
Ом; 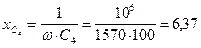 Ом;
Ом;
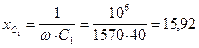 Ом;
Ом;
Сопротивления взаимных индуктивностей:
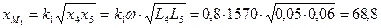 Ом;
Ом;
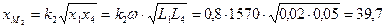 Ом;
Ом;
б). Упрощаем данную схему до трехконтурной, делаем разметку схемы и показываем направления контурных токов.
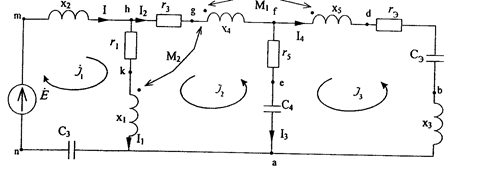
Рис 2. Расчетная схема по методу контурных токов.
Эквивалентное сопротивление 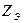 параллельной цепочки
параллельной цепочки 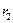 и
и 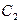 (рис 1)
(рис 1)
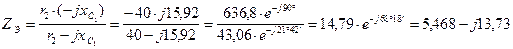 Ом,
Ом,
откуда 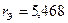 Ом;
Ом; 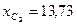 Ом.
Ом.
Для расчета цепи используем метод контурных токов. Метод узловых потенциалов для случаев, когда в цепи индуктивно-связанные катушки не применяются.
Контурными токами считаем 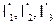 . Уравнения составляем относительно контурных токов. При составлении уравнений очень внимательно следим за знаками у слагаемых, которые обусловлены взаимной индуктивностью. Знак плюс берем, если влияющий ток и направление контурного тока рассматриваемого контура одинаково ориентированы относительно одноименных зажимов. В противном случае берется знак минус.
. Уравнения составляем относительно контурных токов. При составлении уравнений очень внимательно следим за знаками у слагаемых, которые обусловлены взаимной индуктивностью. Знак плюс берем, если влияющий ток и направление контурного тока рассматриваемого контура одинаково ориентированы относительно одноименных зажимов. В противном случае берется знак минус.
в) Составляем систему уравнений.
1й контур:
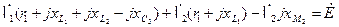
2й контур:
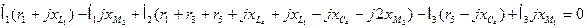
3й контур:
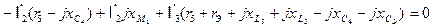
Подставляем в написанное выше уравнения все известные величины:
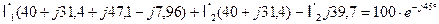
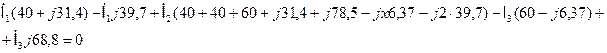
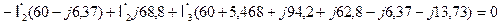
Окончательно получаем
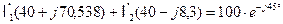
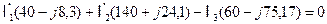
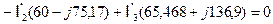
Переводя комплексные числа в показательную форму имеем
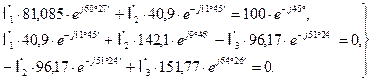 (I)
(I)
Полученную систему трех уравнений с тремя неизвестными представим в матричной форме
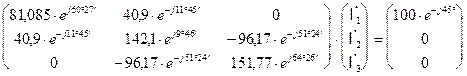
г). Решаем матричное уравнение относительно матрицы
Находим определитель системы (I)
 Определяем алгебраические дополнения элементов матрицы
Определяем алгебраические дополнения элементов матрицы 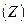
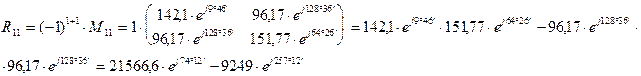
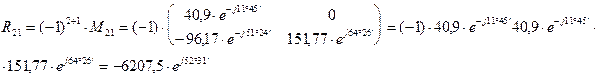
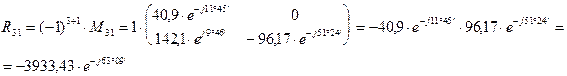
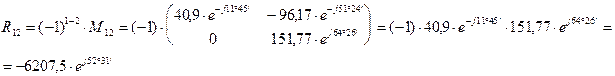
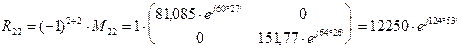
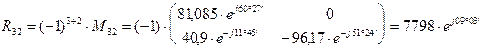
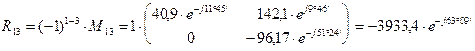
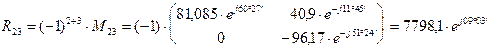
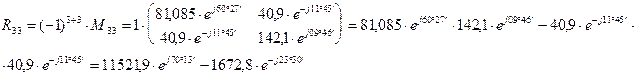
Запишем матрицу относительно тока в развернутой форме
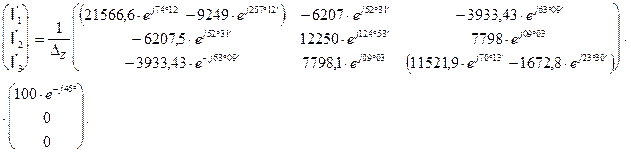
Отсюда
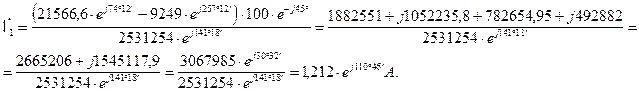
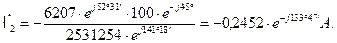
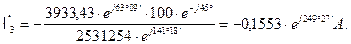
Находим токи в ветвях схемы
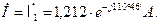
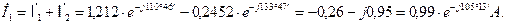
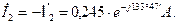
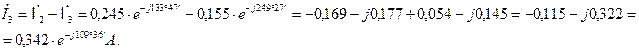
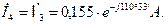
2. Составления баланса активных и реактивных мощностей.
Комплексная мощность 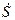 равна произведению комплексного напряжения (э.д.с.) на сопряженный ток
равна произведению комплексного напряжения (э.д.с.) на сопряженный ток
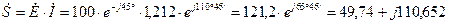 ВА.
ВА.
Источник энергии отдает в цепь активную мощность
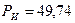 Вт,
Вт,
реактивную мощность
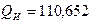 ВАр.
ВАр.
Мощность, потребляемая в активных сопротивлениях
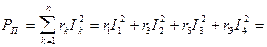
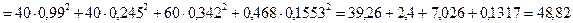 Вт.
Вт.
Погрешность
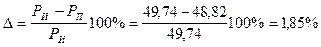
Реактивная мощность, потребляемая в индуктивностях, взаимно-индуктивностях и емкостях
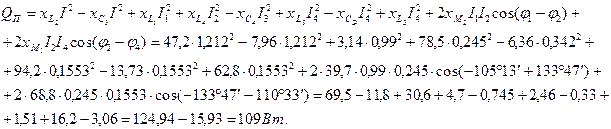
Погрешность
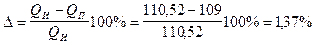
что допустимо (допускается до 8%).
Необходимо отметить, что в формулу для потребляемой реактивной мощности 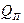 по одному разу входят попарные произведения токов магнитосвязанных друг с другом ветвей, умноженные на удвоенные соответствующие сопротивления взаимоиндукции и на косинусы углов между токами этих ветвей.
по одному разу входят попарные произведения токов магнитосвязанных друг с другом ветвей, умноженные на удвоенные соответствующие сопротивления взаимоиндукции и на косинусы углов между токами этих ветвей.
3. Построение векторной диаграммы токов и топографической диаграммы напряжений.
Выберем масштаб для тока. Наибольшее значение тока, полученное по расчету, равно 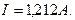
Удобно принять масштаб 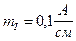 . В этом случае длина максимального вектора тока будет
. В этом случае длина максимального вектора тока будет 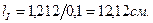
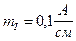 . Длина минимального вектора тока
. Длина минимального вектора тока 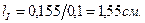 Действительную ось комплексной плоскости направляем вертикально вверх (рис. 4), мнимую горизонтально влево.
Действительную ось комплексной плоскости направляем вертикально вверх (рис. 4), мнимую горизонтально влево.
На графике векторы токов можно строить либо по модулям и начальным фазам (с помощью транспортира), либо по их действительным и мнимым частям. На рис. 4 изображена векторная диаграмма токов. Топографическую диаграмму напряжения на всех элементах электрической цепи в масштабе напряжения, отложив на комплексной плоскости соответствующие отрезки.
Составляем подробную расчетную схему цепи (рис. 3). На этой схеме показываем действительные направления всех токов, э.д.с. и падения напряжений на элементах цепи. Точки, где соединяются элементы цепи обозначаем буквами а, б, с, и т.п.
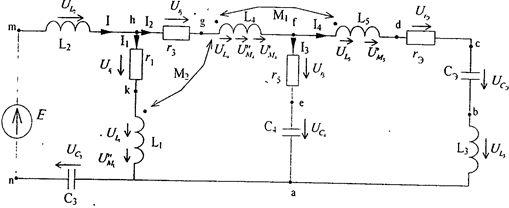
Рис. 3.
Определяем падения напряжения на элементах цепи
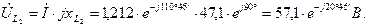
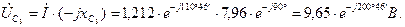
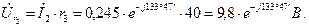
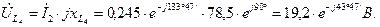
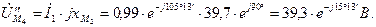
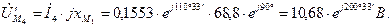
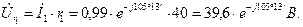
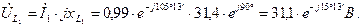
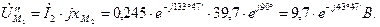
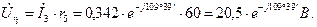
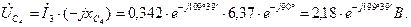
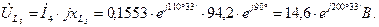
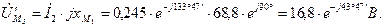
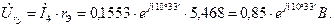
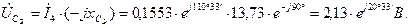
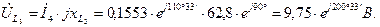
Выбираем масштаб напряжения 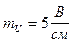 .
.
Построение топографической векторной диаграммы напряжений нужно всегда начинать с разветвления на конце схемы и с точки низшего потенциала. В данной схеме построение начинаем с точки "a", которую поместим в начало координат на комплексной плоскости (рис. 4).
От точка "a" откладываем отрезок ab, представляющий в масштабе напряжения 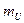 падения напряжения
падения напряжения 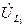 в индуктивности
в индуктивности 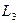 . Отрезок ab равен 19,5 мм. Вектор
. Отрезок ab равен 19,5 мм. Вектор 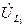 опережает ток
опережает ток 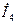 на
на 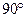 .
.
От точки "b" откладываем вектор падения напряжения 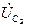 , отстающий от тока
, отстающий от тока 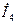 на
на 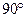 , и определяем точка "с". Отрезок bc равен 4 мм.
, и определяем точка "с". Отрезок bc равен 4 мм.
Из точки "c" откладываем вектор 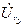 по направлению тока
по направлению тока 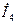 и на графике находим точку d. Отрезок cd равен 1,7 мм.
и на графике находим точку d. Отрезок cd равен 1,7 мм.
Из точки d откладываем вектор падения напряжения 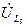 , опережающий ток
, опережающий ток 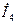 на
на 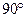 . На графике находим точку f¢. Отрезок df¢ равен 29 мм.
. На графике находим точку f¢. Отрезок df¢ равен 29 мм.
Из точки f¢ откладываем вектор падения напряжения 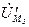 , опережающий ток
, опережающий ток 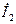 на
на 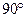 . На графике находим точку f. Отрезок f¢f равен 33,5 мм.
. На графике находим точку f. Отрезок f¢f равен 33,5 мм.
Замыкающий отрезок af равный 41 мм, представляет собой вектор падения напряжения 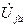 на ветвях, заключенных между узлами a и f. Вектор
на ветвях, заключенных между узлами a и f. Вектор 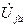 может быть представлен геометрической суммой векторов
может быть представлен геометрической суммой векторов 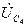 и
и 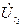 .
.
Точку g¢ на топографической диаграмме находим по падению напряжения в индуктивности 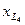 . Вектор
. Вектор 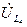 опережающий ток
опережающий ток 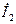 на
на 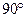 .
.
Из точки g¢ проводим вектор падения напряжения 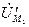 на взаимной индуктивности
на взаимной индуктивности 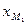 от тока
от тока 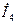 . Вектор
. Вектор 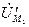 опережающий ток
опережающий ток 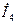 на
на 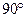 . Находим на графике точку g¢¢. Отрезок g¢g¢¢. Равен 21,4 мм.
. Находим на графике точку g¢¢. Отрезок g¢g¢¢. Равен 21,4 мм.
Из точки g¢¢ откладываем вектор падения напряжения 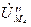 , опережающий ток
, опережающий ток 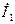 на
на 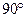 . Находим точку g. Отрезок g¢¢g равен 78,5 мм.
. Находим точку g. Отрезок g¢¢g равен 78,5 мм.
Точку h на топографической диаграмме находим по падению напряжения на сопротивлении 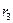 . Вектор
. Вектор 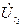 совпадает по направлению с вектором тока
совпадает по направлению с вектором тока 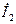 . Точку h можно определить по падению напряжения на индуктивности
. Точку h можно определить по падению напряжения на индуктивности 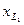 , взаимной индуктивности
, взаимной индуктивности 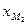 от
от
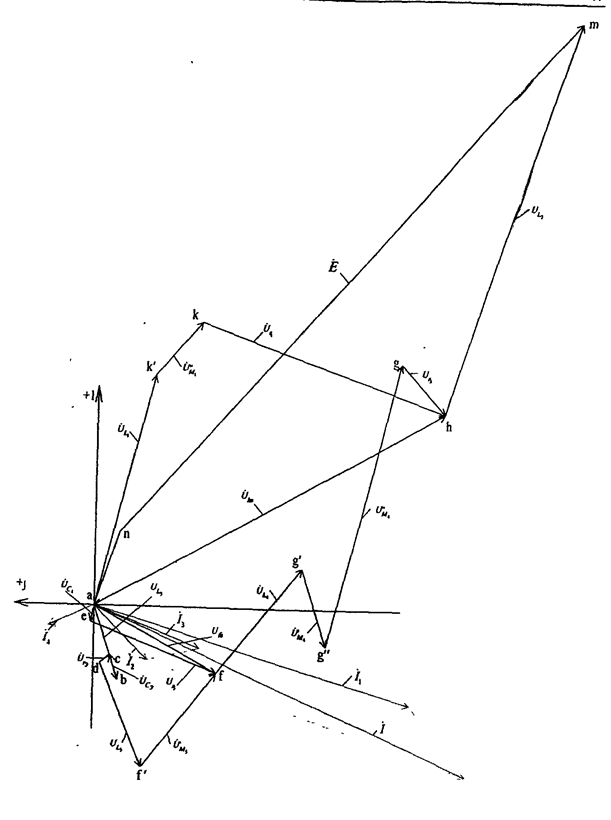
Рис. 4. Векторная диаграмма токов и топографическая диаграмма напряжений при наличии индуктивных связей 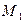 и
и 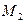 :
: 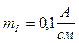 ;
; 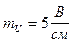 .
.
тока 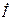 и сопротивлений
и сопротивлений 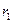 , соотношении
, соотношении 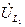 ,
, 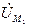 и
и  (рис 4).
(рис 4).
Из точки h откладываем вектор падения напряжения 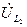 в индуктивности
в индуктивности 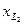 . Находим на графике точку m. Вектор
. Находим на графике точку m. Вектор 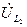 , опережающий ток
, опережающий ток 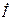 на
на 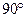 . Отрезок hm равен 114 мм.
. Отрезок hm равен 114 мм.
Точку n на топографической диаграмме находим по падению напряжения 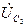 на емкости
на емкости 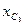 . При этом стрелка падения напряжения
. При этом стрелка падения напряжения 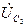 должна смотреть в точку a. Вектор
должна смотреть в точку a. Вектор 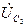 отстает от тока
отстает от тока 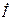 на
на 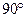 . Отрезок na равен 19,3 мм. Замыкающая nm дает вектор э.д.с.
. Отрезок na равен 19,3 мм. Замыкающая nm дает вектор э.д.с. 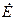 источника.
источника. 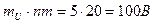 . Отрезок nm направлен под углом -
. Отрезок nm направлен под углом - 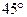 к действительной оси и равен величине э.д.с.
к действительной оси и равен величине э.д.с. 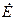 . Это доказывает, что топографическая диаграмма построена верно.
. Это доказывает, что топографическая диаграмма построена верно.
4. Построение волновой диаграммы 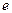 и
и 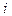 .
.
Э.д.с. 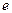 нам задана. Ее мгновенное значение равно
нам задана. Ее мгновенное значение равно 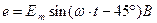 , где
, где 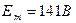 ,
,
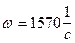 .
.
Для построение этой зависимости на графике определяем масштаб времени и напряжения.
Чтобы на графике было удобно строить синусоиды э.д.с. и тока, выбираем масштаб по оси абсцисс для градуса аргумента 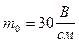 . Тогда целому периоду будет соответствовать отрезок
. Тогда целому периоду будет соответствовать отрезок 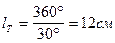 . Этот же отрезок будет соответствовать времени
. Этот же отрезок будет соответствовать времени 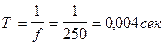 . Синусоида э.д.с.
. Синусоида э.д.с. 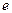 сдвинута вправо относительно начала координат на угол
сдвинута вправо относительно начала координат на угол 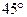 или на
или на 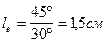 . Амплитуда э.д.с.
. Амплитуда э.д.с. 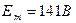 . Выбираем масштаб
. Выбираем масштаб 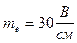 . Кривую
. Кривую 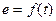 (рис 5) строим по точкам по значениям синусов для углов
(рис 5) строим по точкам по значениям синусов для углов 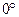 ,
, 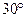 ,
, 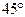 ,
, 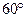 и
и 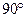 (или
(или 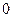 ,
, 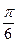 ,
, 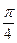 ,
, 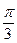 и
и 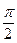 ). Например, при
). Например, при 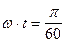 ,
, 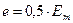 .
.
В результате расчета получено значение тока, протекающего через источник 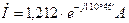 .
.
Мгновенное значение этого тока 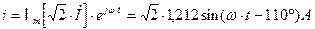 , где
, где 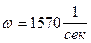 .
.
Синусоида тока 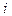 сдвинута вправо относительно начала координат на угол
сдвинута вправо относительно начала координат на угол 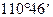 или на
или на 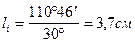 .
.
Масштаб тока выбираем 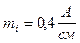 .
.
Кривую 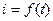 строем по точкам (рис. 5).
строем по точкам (рис. 5).
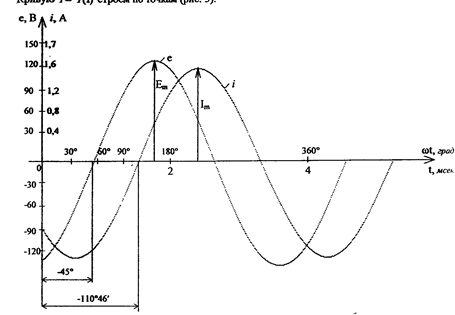
Рис. 5. Кривые 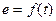 и
и 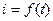
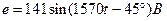 ,
,
II. Метод пропорционального пересчета. Приведен пример расчета для схемы (рис. 6), в которой взаимная индуктивность убрана.
Типовой расчет будем производить для заданной схемы при развязанной взаимной индуктивности. Развязку сделать самостоятельно!!!
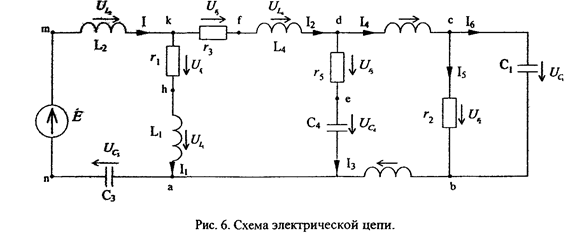
1. Делаем разметку схемы (рис. 6).
2. Задаемся произвольной величиной 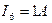 .
.
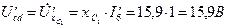 .
.
Масштаб для тока выбираем 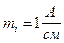 , масштаб для напряжения
, масштаб для напряжения 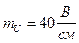 .
.
Построение векторной диаграммы начинаем с точки b (рис. 7). Откладываем в произвольном направлении ток 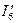 , и проводим из точки b вектор
, и проводим из точки b вектор 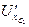 , который отстает от тока
, который отстает от тока 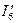 на
на 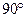 .
.
3. Находим ток 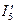
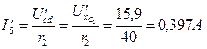 .
.
Откладываем ток 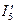 на диаграмме по напряжению
на диаграмме по напряжению 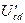 .
.
4. Из диаграммы определяем ток 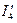 как сумму
как сумму 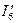 и
и 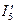 .
.
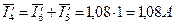 .
.
5. 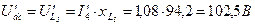 .
.
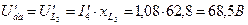 .
.
Из точки C откладываем вектор 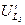 , который опережает ток
, который опережает ток 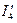 .
.
Находим точку d, вектор 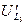 проводим к точке b, опережает
проводим к точке b, опережает 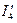 на
на 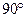 . Находим точку a.
. Находим точку a.
6. Из диаграммы - замыкающая между точками d и a, есть 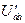
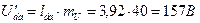 .
.
7. Определяем полное сопротивление ветви da
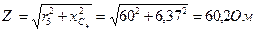 .
.
Учитывая п.6 и п.7 получаем
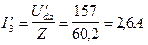 .
.
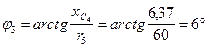 .
.
Откладываем вектор тока 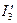 , опережающий напряжение
, опережающий напряжение 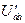 на угол
на угол 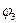 .
.
8. Находим 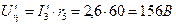 ,
,
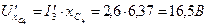 .
.
Откладываем полученные векторы на диаграмме и находим точку e.
9. Из диаграммы находим ток 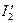 , складываем геометрически
, складываем геометрически 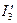 и
и 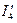 .
.
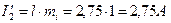 .
.
10. На диаграмме находим точки f и k, предварительно отложив векторы напряжения
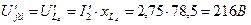 - от точки d против часовой стрелки на
- от точки d против часовой стрелки на 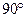 к
к 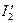 .
.
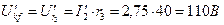 - от точки f по току
- от точки f по току 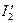 .
.
11. Из векторной диаграммы замыкающаяся между точками k и a есть напряжение 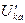
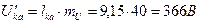 .
.
12. Находим ток 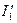 и откладываем его на диаграмме
и откладываем его на диаграмме
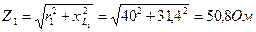 .
.
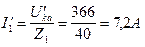 .
.
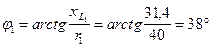
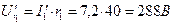 ,
,
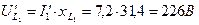 .
.
Откладываем вектор  и
и 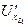 , находим точку h.
, находим точку h.
13. Из диаграммы определяем ток 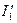 складываем геометрически
складываем геометрически 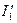 и
и 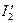
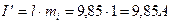 .
.
14. 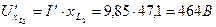 ,
, 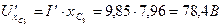 .
.
Из точки k откладываем вектор 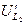 , который опережает ток
, который опережает ток 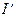 на
на 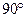 . Находим точку m.
. Находим точку m.
Вектор 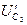 проводим к точке a по часовой стрелке на
проводим к точке a по часовой стрелке на 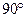 к току
к току 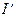 . Находим точку n.
. Находим точку n.
15. Из диаграммы - 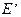 , замыкающая между точками m и n
, замыкающая между точками m и n
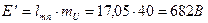 .
.
Так как эта величена не равна заданной э.д.с. 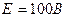 ,то все значения токов и напряжений надо пересчитать по условию прямой пропорциональности.
,то все значения токов и напряжений надо пересчитать по условию прямой пропорциональности.
Коэффициент пересчета 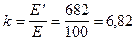 .
.
По условию задачи 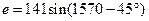 , то есть имеется начальная фаза, определяемая углом -
, то есть имеется начальная фаза, определяемая углом - 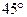 . По этому на топографической векторной диаграмме наносим действительную и мнимые оси, таким образом, чтобы вектор
. По этому на топографической векторной диаграмме наносим действительную и мнимые оси, таким образом, чтобы вектор 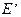 составлял с действительной осью
составлял с действительной осью 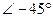 .
.
В результате этого токи и напряжения можно записать в комплексной форме, при этим модули должны быть уменьшены в 6,82 раза.
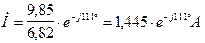
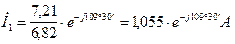
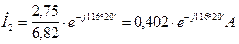
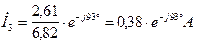
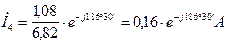
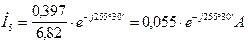
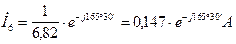
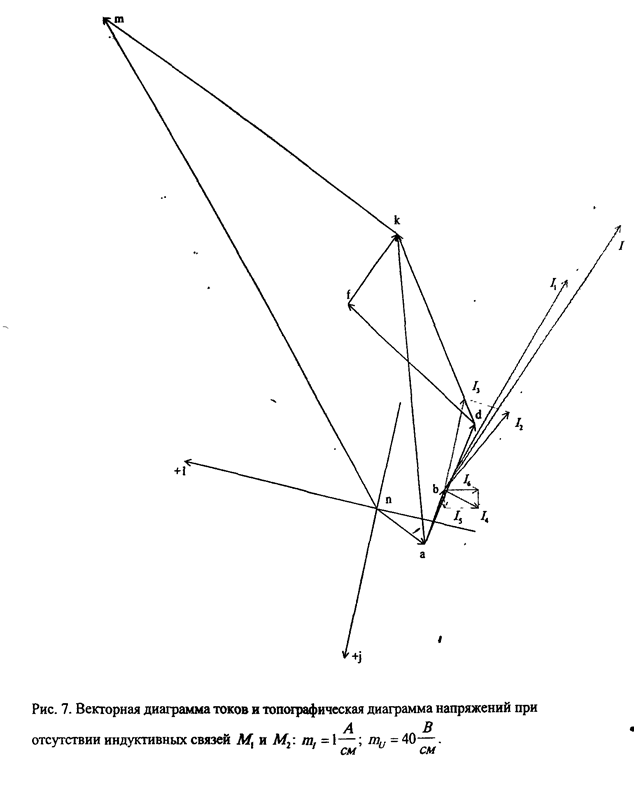
Рис. 7. Векторная диаграмма токов и топографическая диаграмма напряжений при отсутствии индуктивных связей 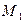 и
и 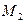 :
: 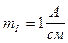 ;
; 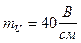 .
.
Искомые напряжения
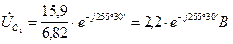
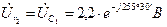
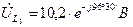
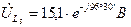
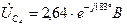
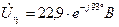
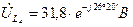
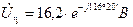
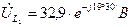
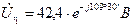
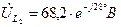
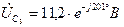
Диаграмма и для действительных величин останется такой же изменится только ее масштаб. Поэтому на рис. 7 векторы обозначают 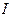 ,
, 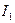 ,
, 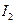 и т.д., а не
и т.д., а не 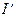 ,
, 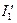 ,
, 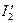 и т.д.
и т.д.
Составление баланса активных и реактивных мощностей. Как известно, комплексная мощность 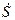 равна произведению комплексной э.д.с. на сопряженный комплексный ток.
равна произведению комплексной э.д.с. на сопряженный комплексный ток.
Мощность источника энергии
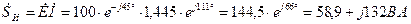
Отсюда 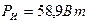 ,
,
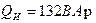 .
.
Мощность, развиваемая в активных сопротивлениях
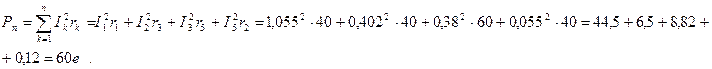 Погрешность
Погрешность
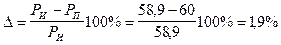
допускается 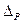 до 5%.
до 5%.
Реактивная мощность в индуктивностях
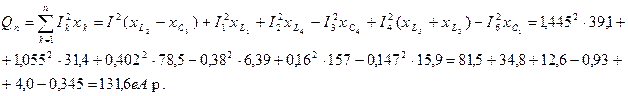
Погрешность
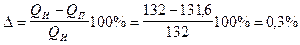
Допускается 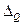 до 8%.
до 8%.
Вопросы по расчету при защите.
Определить аналитически показание вольтметра, подключенного к точкам e и d цепи. Показать на топографической диаграмме напряжений вектор 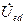 .
.
Включить ваттметр в цепь так, чтобы он измерял мощность, затрачиваемую на выделение тепла в сопротивлении 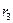 .
.
Произвести развязку индуктивных связей.
Определить сопротивление 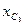 , если частота тока в цепи равна
, если частота тока в цепи равна 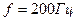 .
.
Определить показание ваттметра, если через него проходит ток ________напряжения подключена к точкам k и d (рис.)
___________ выражение для мгновенного значения напряжения U _____________ зависимости 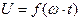 .
.
 2015-05-26
2015-05-26 389
389






