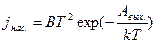 - плотность тока насыщения при термоэлектронной эмиссии (формула Ричардсона –Дешмена);
- плотность тока насыщения при термоэлектронной эмиссии (формула Ричардсона –Дешмена);
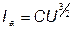 - закон «трех вторых» (Ленгмюра и Богуславского).
- закон «трех вторых» (Ленгмюра и Богуславского).
Примеры решения задач.
Пример 1.
Определить напряжённость поля, создаваемого зарядом, равномерно распределённым по тонкому прямому стержню с линейной плотностью 200 нКл/м, в точке, лежащей на перпендикуляре, восстановленном в середине стержня, на расстоянии 40 см от его середины. Длина стержня 60 см.
| Дано: τ=2.10-7 Кл/м l =0.6 м b=0.4 м | Решение:
Разобьем стержень на бесконечно малые элементы dl=dy; y – координата данного элемента. Заряд элемента dq= τ dy можно считать точечным. Напряженность поля, созданного зарядом dq в точке А на расстоянии r от заряда, равна:
|
Где
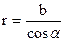 ; (2)
; (2)
α – угол между перпендикуляром к стержню и радиус-вектором r элемента стержня, проведенным из точки А. Направление вектора напряженности см. на рисунке.

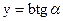 ,
,  то
то 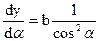 , или:
, или:
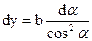 . (3)
Найдем проекции dE на координатные оси:
. (3)
Найдем проекции dE на координатные оси:
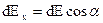 ;
; 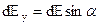 , (4)
Наконец, проекции полной напряженности на оси рассчитываются интегрированием:
, (4)
Наконец, проекции полной напряженности на оси рассчитываются интегрированием:
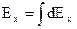 ;
; 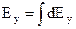 , (5)
причем интегрирование производится по всей длине стержня. Здесь использован принцип суперпозиции в проекциях на оси. Полная напряженность вычисляется по теореме Пифагора:
, (5)
причем интегрирование производится по всей длине стержня. Здесь использован принцип суперпозиции в проекциях на оси. Полная напряженность вычисляется по теореме Пифагора:
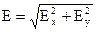 . (6)
С учетом (1) – (4) получим из (5):
. (6)
С учетом (1) – (4) получим из (5):
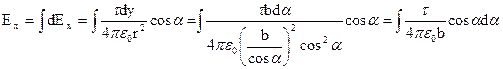 , (7)
, (7)
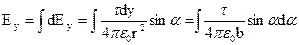 .
Постоянную величину
.
Постоянную величину 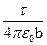 выносим за знак интеграла и проставим пределы интегрирования: угол α изменяется от (–α0) до α0, где
выносим за знак интеграла и проставим пределы интегрирования: угол α изменяется от (–α0) до α0, где 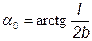 . Далее, первообразная функция от
. Далее, первообразная функция от 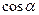 - это
- это 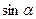 , а от
, а от 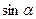 -
- 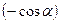 . Тогда
. Тогда
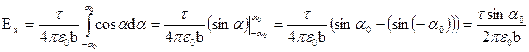 ,
,
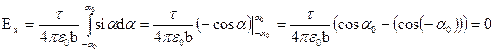 .
Окончательно получаем для напряженности:
.
Окончательно получаем для напряженности:
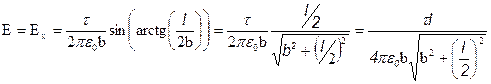 ,
,
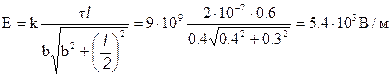 .
.
Пример 2.
Определить потенциал поля, создаваемого зарядом, равномерно распределённым по тонкому прямому стержню с линейной плотностью 200 нКл/м, в точке, лежащей на перпендикуляре, восстановленном в одном из концов стержня, на расстоянии 40 см от него. Длина стержня 30 см.
| Дано: τ=2.10-7 Кл/м l =0.3 м b=0.4 м | Решение:
Разобьем стержень на бесконечно малые элементы dl=dy; y – координата данного элемента. Заряд элемента dq= τ dy можно считать точечным. Потенциал поля, созданного зарядом dq в точке А на расстоянии r от заряда, равен:
Где
 Сейчас читают про:
|
 2015-05-26
2015-05-26 433
433

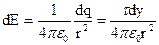 , (1)
, (1)
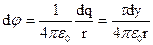 , (1)
, (1)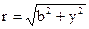 . (2)
. (2)





