Экспериментальный метод можно пояснить с помощью установки, состоящей из стеклянного сосуда большой емкости (рис.3.1), соединенного с манометром, который может соединяться с атмосферой или с насосом. Разность между давлением воздуха в сосуде и атмосферным давлением измеряется открытым жидкостным манометром, одно колено которого соединено с сосудом.
Обозначим атмосферное давление во время опыта 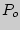 , абсолютную температуру воздуха в комнате
, абсолютную температуру воздуха в комнате 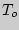 , объем газа
, объем газа  , а массу газа в сосуде
, а массу газа в сосуде 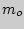 . Если, разобщив баллон с атмосферой, накачать в него насосом небольшое количество воздуха, давление в сосуде повысится.
. Если, разобщив баллон с атмосферой, накачать в него насосом небольшое количество воздуха, давление в сосуде повысится.
При любой массе газа он занимает в сосуде весь объем 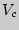 . При накачивании или выпускании воздуха масса его в сосуде меняется, и уравнения изопроцессов становятся непригодными. Но они сохраняет свой вид, если рассматривать удельный объем
. При накачивании или выпускании воздуха масса его в сосуде меняется, и уравнения изопроцессов становятся непригодными. Но они сохраняет свой вид, если рассматривать удельный объем 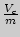 . Объем сосуда остается неизменным, поэтому увеличение массы газа в сосуде приводит к уменьшению удельного объема газа.
. Объем сосуда остается неизменным, поэтому увеличение массы газа в сосуде приводит к уменьшению удельного объема газа.
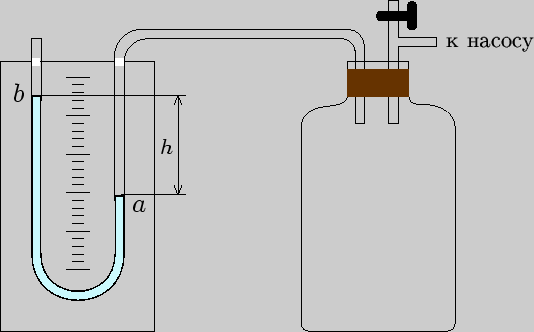
Рис. 3.1
При помощи насоса в сосуд накачивается некоторое количество газа массы 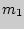 , занимающего некоторый объем
, занимающего некоторый объем 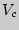 . Его удельный объем
. Его удельный объем 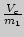 .
.
При накачивании газа совершается работа внешними силами. Если накачивать газ быстро, то теплообменом газа с окружающей средой через стенки можно пренебречь и считать процесс адиабатическим. За счет работы внешних сил увеличится внутренняя энергия газа, он нагреется до температуры 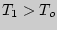 , а давление его станет равным
, а давление его станет равным 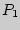 . Установится первое состояние газа. Процесс накачивания изображен на рис.3.2 кривой
. Установится первое состояние газа. Процесс накачивания изображен на рис.3.2 кривой 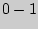 . На оси абсцисс указаны удельные объемы.
. На оси абсцисс указаны удельные объемы.
После прекращения накачивания неизменная масса 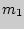 , изохорически охлаждается до комнатной температуры
, изохорически охлаждается до комнатной температуры 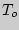 зa счет теплообмена. Из-за малой теплопроводности стекла это продолжается
зa счет теплообмена. Из-за малой теплопроводности стекла это продолжается 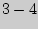 минуты. Изохорический процесс на рис.3.2 изображен прямой
минуты. Изохорический процесс на рис.3.2 изображен прямой 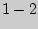 . В конце изохорического процесса устанавливается второе состояние газа с давлением
. В конце изохорического процесса устанавливается второе состояние газа с давлением 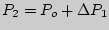 , температурой
, температурой 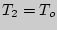 и удельным объемом
и удельным объемом 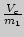 .
.
Здесь 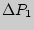 -- избыточное над атмосферным давление газа, измеряемое манометром во втором состоянии, то есть после накачивания и установления равновесного состояния газа в сосуде.
-- избыточное над атмосферным давление газа, измеряемое манометром во втором состоянии, то есть после накачивания и установления равновесного состояния газа в сосуде.
Если теперь на короткое время открыть кран, часть газа выйдет из сосуда, давление его станет равным атмосферному, а температура газа в сосуде понизится. Этот процесс можно считать адиабатическим вследствие быстроты (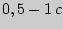 ). Состояние газа при открытом кране является третьим состоянием и характеризуется параметрам
). Состояние газа при открытом кране является третьим состоянием и характеризуется параметрам 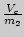 (
(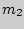 -- масса газа, оставшегося в сосуде),
-- масса газа, оставшегося в сосуде), 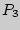 ,
, 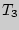 , причем
, причем 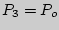 , а
, а 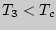 .
.
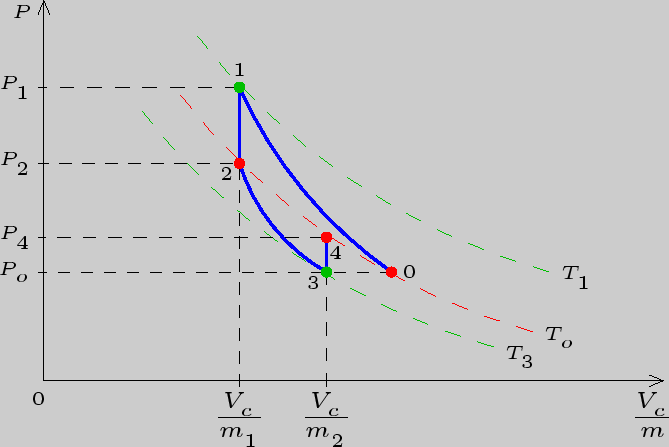
Рис. 3.2
После этого в течение 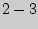 минут происходит нагревание газа в сосуде за счет теплообмена, пока температура не сравняется с комнатной; давление газа при этом возрастает. Новое установившееся состояние является четвертым и описывается параметрами
минут происходит нагревание газа в сосуде за счет теплообмена, пока температура не сравняется с комнатной; давление газа при этом возрастает. Новое установившееся состояние является четвертым и описывается параметрами 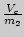 ,
, 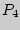 ,
, 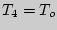 . При этом
. При этом 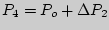 . Здесь
. Здесь 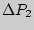 -- избыточное над внешним давление, измеряемое после того, как кран закрыт и снова наступило равновесное состояние газа. Графики описанных процессов изображены на рис.3.2. Пунктирные кривые -- изотермы.
-- избыточное над внешним давление, измеряемое после того, как кран закрыт и снова наступило равновесное состояние газа. Графики описанных процессов изображены на рис.3.2. Пунктирные кривые -- изотермы.
Для вывода расчетной формулы рассмотрим часть графика, а именно участки 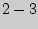 и
и 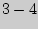 и учтем, что точки 2 и 4 лежат на одной изотерме. Переход из второго состояния в третье происходит адиабатически, для него справедливо уравнение Пуассона:
и учтем, что точки 2 и 4 лежат на одной изотерме. Переход из второго состояния в третье происходит адиабатически, для него справедливо уравнение Пуассона:
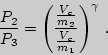
| (5) |
При 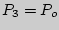 и
и 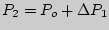 , получаем
, получаем
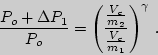
| (6) |
Процесс на участке 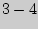 изохорический, а точки 2 и 4 лежат на одной изотерме, поэтому можно применить уравнение Бойля - Мариотта для удельных объемов:
изохорический, а точки 2 и 4 лежат на одной изотерме, поэтому можно применить уравнение Бойля - Мариотта для удельных объемов:
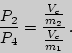
| (7) |
Объединяя (6) и (7), получим:
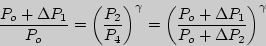
| (8) |
или
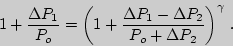
| (9) |
Отсюда
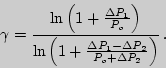
| (10) |
Если 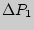 мало по сравнению с
мало по сравнению с 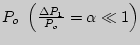 , то
, то
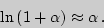
Используя это соотношение, получим:
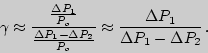
| (11) |
Величина избыточного давления измеряется разностью уровней жидкости в манометре (см. рис.3.1): 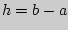 .
.
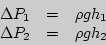
| (12) |
Здесь 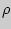 -- плотность жидкости в манометре.
-- плотность жидкости в манометре.
При 
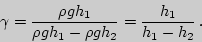
| (13) |
Полученное соотношение является расчетной формулой для 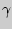 в данной работе. Таким образом для нахождения искомой величины следует измерить
в данной работе. Таким образом для нахождения искомой величины следует измерить 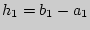 и
и 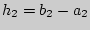 .
.
 2015-05-29
2015-05-29 312
312






