Исследовать функцию 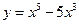 и построить её график
и построить её график
1. Область определения D многочлена интервал 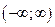
2. Определим нули функции. В данном случае это возможно
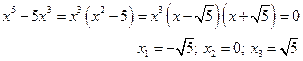
3. Функция нечётная, так как 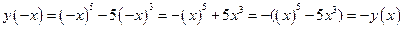
4. Исследуем функцию на асимптотическое поведение. Многочлен не имеет асимптот.
5. Определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. У многочлена все критические точки стационарные в них 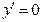 . Отсюда
. Отсюда 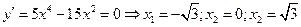
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | - 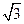 | 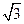 | |||||
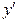 | + | - | - | + | |||
| y | 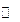 | -10.4 | 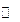 | 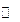 | 10.4 |  |
Используя алгоритм нахождения локальных экстремумов с помощью первой производной
получаем. При х =- 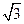 локальный максимум, при х=0 экстремума нет, при х=
локальный максимум, при х=0 экстремума нет, при х= 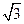 локальный минимум.
локальный минимум.
6. Исследуем функцию на выпуклость. Находим точки подозрительные на перегиб
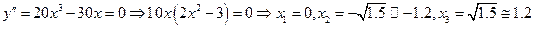
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | -1.2 | 1.2 | |||||
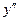 | - | + | - | + | |||
| y | -6.2 | 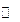 | 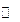 | 6.2 | 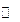 |
Используя алгоритм нахождения точек перегиба с помощью второй производной, получаем. При х=- 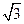 , при х=0, при х=
, при х=0, при х= 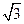 - перегиб графика функции.
- перегиб графика функции.
7. График пересекает ось ОУ в точке (0,0).
8. СТРОИМ ГРАФИК.
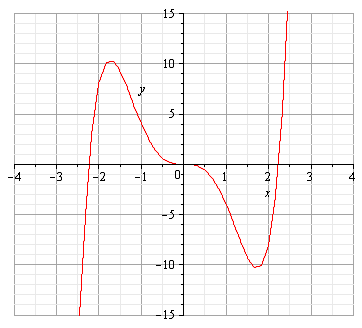
Исследовать функцию 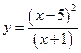 и построить её график
и построить её график
1. Область определения D функции- объединение интервалов 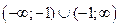
2.Определим нули функции. В данном случае это возможно 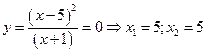
3.Функция общего вида
4. Исследуем функцию на асимптотическое поведение. Асимптота это прямая, к которой неограниченно приближается график функции при 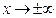 . Наклонная асимптота имеет уравнение
. Наклонная асимптота имеет уравнение 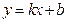 . Алгоритм нахождения параметров
. Алгоритм нахождения параметров 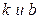 известен
известен
Сначала всегда определяем 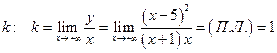 .
.
Затем
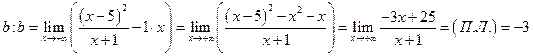
Уравнение наклонной асимптоты найдено 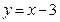
Проверим, имеет ли данная функция вертикальную асимптоту. Вертикальная асимптота –
Прямая, имеющая уравнение 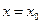 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 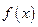 если
если 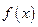 бесконечно большая при
бесконечно большая при 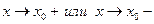 .
.
Так как 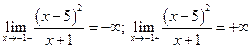 , то
, то
прямая 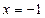 является вертикальной асимптотой.
является вертикальной асимптотой.
5.с помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Стационарными точками являются точки в которых 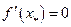 :
: 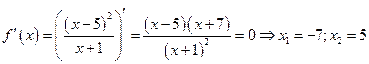
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | -7 | ||||
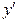 | + | - | + | ||
| y | 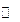 | -24 | 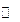 | 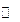 |
Используя алгоритм нахождения локальных экстремумов с помощью первой производной
получаем. При х=-7 локальный максимум, при х=5 локальный минимум.
2. С помощью второй производной 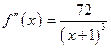 исследуем функцию на выпуклость. Находим точки подозрительные на перегиб
исследуем функцию на выпуклость. Находим точки подозрительные на перегиб
В этих точках либо 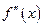 не существует, либо
не существует, либо 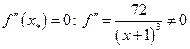 . Только одна точка подозрительна на перегиб
. Только одна точка подозрительна на перегиб 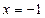 .
.
Для определения знаков второй производной слева и справа от этой точки применяем метод интервалов и заполняем соответствующую таблицу
| x | -1 | ||
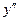 | 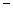 | + | |
| y | 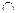 | нет | 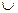 |
3. График пересекает ось ОУ в точке (5,0).
4. СТРОИМ ГРАФИК.
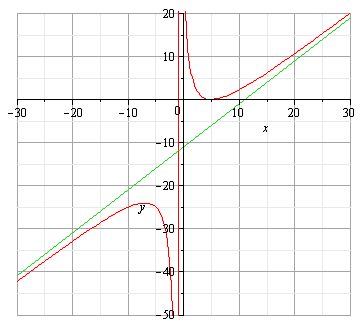
Исследовать функцию 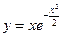 и построить её график
и построить её график
1. Область определения D функции интервал 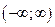
2.Определим нули функции. В данном случае это возможно
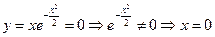
3.Так как 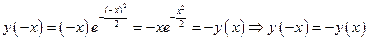 , то
, то 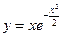
функция общего вида.
4. Исследуем функцию на асимптотическое поведение. Асимптота это прямая, к которой неограниченно приближается график функции при 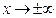 . Наклонная асимптота имеет уравнение
. Наклонная асимптота имеет уравнение 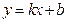 . Алгоритм нахождения параметров
. Алгоритм нахождения параметров 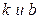 известен
известен
Сначала всегда определяем 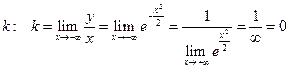 .
.
Затем 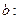
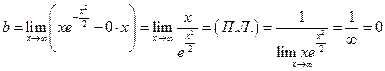
П. Уравнение наклонной асимптоты найдено 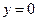
Так как функция 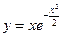 непрерывна, то вертикальных асимптот нет.
непрерывна, то вертикальных асимптот нет.
5.С помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Стационарными точками являются точки в которых 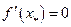 :
:
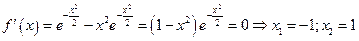
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | -1 | ||||
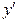 | 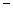 | + | 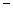 | ||
| y | 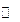 | -0,6 |  | 0,6 |  |
Используя алгоритм нахождения локальных экстремумов с помощью первой производной
получаем. При х=-1 локальный минимум, при х=1 локальный максимум.
5. С помощью второй производной исследуем функцию на выпуклость. Находим точки подозрительные на перегиб. В этих точках либо  не существует, либо
не существует, либо 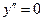 .
.
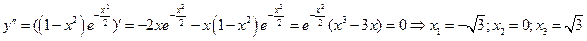
Для определения знаков второй производной слева и справа от этих точек применяем метод интервалов и заполняем соответствующую таблицу
| x | - 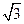 | 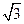 | |||||
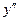 | 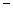 | + | 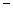 | + | |||
| y | 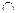 | нет | 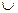 |
6. График пересекает ось ОУ в точке (0,0).
7. СТРОИМ ГРАФИК.
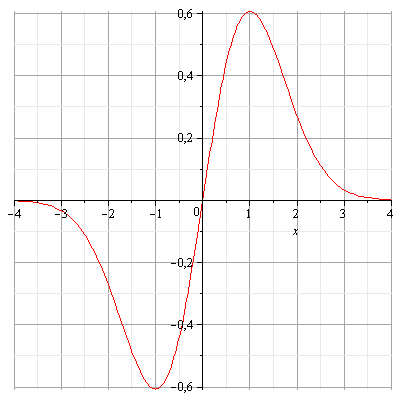
Исследовать функцию 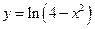 и построить её график. Если есть возможность
и построить её график. Если есть возможность
упростить выражение функции, то это нужно проделать. Упрощаем
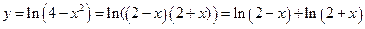
1. Область определения D функции- интервал 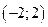
2.Определим нули функции. В данном случае это возможно
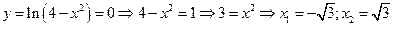
3.Функция четная, так как 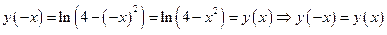
4. Исследуем функцию на асимптотическое поведение. Наклонная асимптота это прямая, к которой неограниченно приближается график функции при 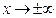 . В нашем случае переменная
. В нашем случае переменная 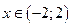 и поэтому не может стремиться к бесконечности. Наклонных асимптот нет.
и поэтому не может стремиться к бесконечности. Наклонных асимптот нет.
Проверим, имеет ли данная функция вертикальную асимптоту. Прямая, имеющая уравнение 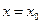 будет Вертикальной асимптотой – если
будет Вертикальной асимптотой – если 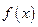 бесконечно большая при
бесконечно большая при 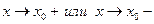 .
.
Так как 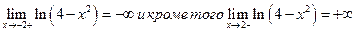 , то
, то
прямые 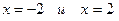 являются вертикальными асимптотами.
являются вертикальными асимптотами.
5. С помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Критические точки функции это точки в которых производная либо не существует либо равна нулю. Стационарными точками являются точки в которых 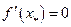 :
:
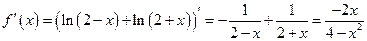 =0;
=0; 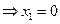
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | |||
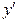 | + | 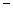 | |
| y | 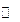 | 1,4 | 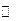 |
Используя алгоритм нахождения локальных экстремумов с помощью первой производной
получаем. При х=0 локальный максимум.
8. С помощью второй производной исследуем функцию на выпуклость. Находим точки подозрительные на перегиб. В этих точках либо 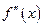 не существует, либо
не существует, либо 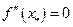 .
.
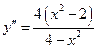
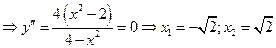
Для определения знаков второй производной слева и справа от этих точек применяем метод интервалов и заполняем соответствующую таблицу
| x | 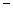 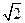 | 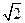 | |||
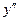 | + | 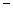 | + | ||
| y | 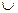 | 0.7 | 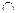 | 0.7 | 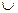 |
9. График пересекает ось ОУ в точке ( ;0).
;0).
10. СТРОИМ ГРАФИК.
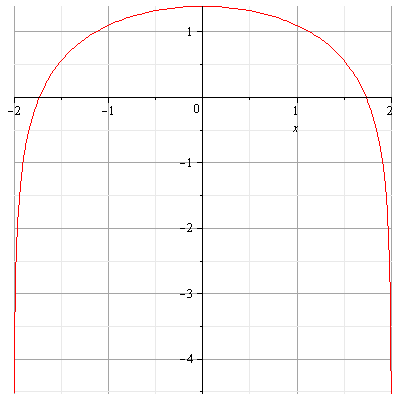
Исследовать функцию 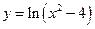 и построить её график. Если есть возможность
и построить её график. Если есть возможность
упростить выражение функции, то это нужно проделать. Упрощаем
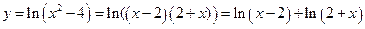
1. Область определения D функции- объединение интервалов 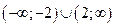
2.Определим нули функции. В данном случае это возможно
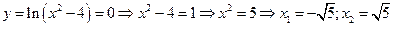
3.Функция четная, так как 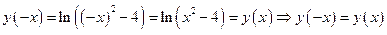
4. Исследуем функцию на асимптотическое поведение. Наклонная асимптота это прямая, к которой неограниченно приближается график функции при 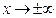 . Для вычисления
. Для вычисления
наклонной асимптоты применяем соответствующий алгоритм
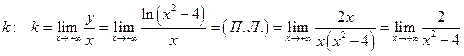
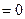
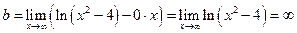 . Вывод: наклонных асимптот нет.
. Вывод: наклонных асимптот нет.
Проверим, имеет ли данная функция вертикальную асимптоту. Прямая, имеющая уравнение 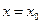 будет вертикальной асимптотой, если
будет вертикальной асимптотой, если 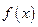 бесконечно большая при
бесконечно большая при 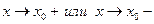 .
.
Так как 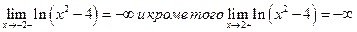 , то
, то
прямые 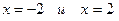 являются вертикальными асимптотами.
являются вертикальными асимптотами.
5. С помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Критические точки функции это точки в которых производная либо не существует либо равна нулю. Стационарными точками являются точки, в которых 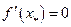 :
:
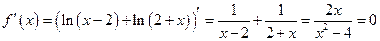
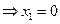 , но
, но
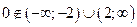
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | -2 | ||||
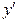 | 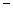 | нет | нет | + | |
| y | 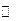 | нет | нет | 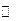 |
Используя алгоритм нахождения локальных экстремумов с помощью первой производной
получаем. Нет критических точек 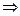 нет локальных экстремумов.
нет локальных экстремумов.
11. С помощью второй производной исследуем функцию на выпуклость. Находим точки подозрительные на перегиб. В этих точках либо 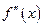 не существует, либо
не существует, либо 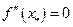 .
.
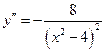 ; В D
; В D 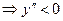
Поэтому в D функция выпукла вверх.
12. График не пересекает ось ОУ так как х=0 не принадлежит области задания D.
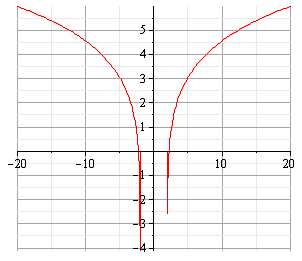
13. СТРОИМ ГРАФИК.
 2015-05-22
2015-05-22 1134
1134







