Равновесие на рынке рисковых активов

Теперь мы можем сформулировать условие равновесия для рынка рисковых активов. Вспомним, что на рынке активов с исключительно гарантированными доходами все активы, как мы видели, должны приносить одинаковую норму дохода. Здесь соблюдается тот же принцип: все активы, с учетом поправки на риск, должны приносить одну и ту же норму дохода.

Загвоздка - в поправке на риск. Как это сделать? Ответ дан проведенным ранее анализом оптимального выбора. Вспомним, что мы рассматривали выбор оптимального портфеля, содержащего один безрисковый и один рисковый актив. Рисковый актив интерпретировался нами как взаимный фонд - диверсифицированный портфель, включающий в себя много рисковых активов. В настоящем параграфе мы предположим, что этот портфель состоит только из рисковых активов.

Тогда можно отождествить ожидаемый доход на этот рыночный портфель рисковых активов с ожидаемым рыночным доходом, 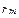, а стандартное отклонение рыночного дохода с рыночным риском, 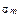. Доход на надежный актив обозначим как 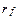, доход, "свободный" от риска.

Как видно было из уравнения (13.1), цена риска, p, задана формулой

.

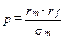Выше было сказано, что величина риска, характеризующая данный актив i, взятая по отношению к общему рыночному риску, обозначается как 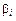. Это означает, что для измерения общей величины риска, характеризующей актив i, следует умножить 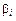на рыночный риск, 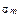. Следовательно, общая величина риска по данному активу задается .

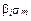Каковы издержки несения этого риска? Просто умножьте общую величину риска, 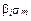, на цену риска. Это и даст нам поправку на риск:

поправка на риск =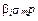

=

= .

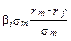
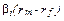Теперь мы можем сформулировать условие равновесия рынков рыночных активов: в равновесии все активы должны приносить одинаковую, с учетом поправки на риск, норму дохода. Логика здесь та же, что и в главе 12: если бы один актив приносил, с учетом поправки на риск, более высокую норму дохода, чем другой, то все захотели бы владеть активом с более высокой, с учетом поправки на риск, нормой дохода. Следовательно, в равновесии нормы дохода, взятые с учетом поправки на риск, должны уравниваться.

Если имеется два актива i и j с ожидаемыми доходам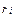и и 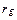и бетам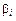и и 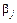, то в равновесии должно удовлетворяться следующее условие:

.

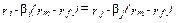Это уравнение говорит нам, что в равновесии нормы дохода с учетом поправки на риск для двух активов должны быть одинаковы - поправка на риск здесь дана как произведение общей величины риска актива на цену риска.

Чтобы выразить это условие по-другому, заметим следующее. Для надежного актива, по определению, должно соблюдаться 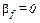. Причина этого состоит в том, что риск по данному активу равен нулю, а 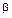измеряет величину риска, характеризующую актив. Таким образом, для любого актива i должно соблюдаться

.

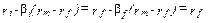После преобразований это уравнение говорит о том, что

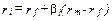
или что ожидаемый доход на любой актив должен равняться сумме дохода на надежный актив и поправки на риск. Этот последний член отражает тот добавочный доход, получения которого требуют люди в обмен на согласие нести риск, воплощенный в данном активе. Это уравнение является главным результатом Модели Ценообразования на Капитальные Активы (МЦКА), имеющей многочисленные применения при изучении финансовых рынков.