Нехай в області D задано функцію 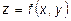 та лінію L задану рівнянням
та лінію L задану рівнянням 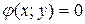 . Задача полягає в знаходженні такої точки
. Задача полягає в знаходженні такої точки 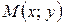 на лінії L, в якій значення функції
на лінії L, в якій значення функції 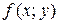 є найбільшим або найменшим порівняно із значеннями цієї функції в інших точках лінії L. Такі точки М називають точками умовного екстремуму функції
є найбільшим або найменшим порівняно із значеннями цієї функції в інших точках лінії L. Такі точки М називають точками умовного екстремуму функції 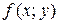 на лінії L.
на лінії L.
На відміну від звичайного екстремуму значення функції в точці умовного екстремуму порівнюється із значеннями цієї функції не в усіх точках області D,а лише в точках, які лежать на лінії L.
Назва «умовний екстремум» пов’язана з тим, що змінні х та у мають додаткову умову: 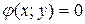 .
.
Рівняння 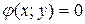 називається рівнянням зв’язку; якщо це рівняння можна розв’язати відносно однієї змінної, наприклад у:
називається рівнянням зв’язку; якщо це рівняння можна розв’язати відносно однієї змінної, наприклад у: 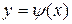 , то, підставляючи замість у значення
, то, підставляючи замість у значення 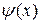 у функцію
у функцію 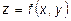 , дістаємо функцію однієї змінної
, дістаємо функцію однієї змінної 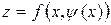 . Оскільки додаткова умова врахована, то задача знаходження умовного екстремуму зводиться до задачі на звичайний екстремум функції однієї змінної.
. Оскільки додаткова умова врахована, то задача знаходження умовного екстремуму зводиться до задачі на звичайний екстремум функції однієї змінної.
Проте не завжди можна розв’язати рівняння зв’язку відносно у чи х. тоді розв'язують поставлену задачу так.
Розглянемо функцію 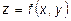 , де
, де 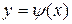 , як складену функцію. З необхідної умови екстремуму випливає, що в точках екстремуму
, як складену функцію. З необхідної умови екстремуму випливає, що в точках екстремуму 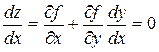 .
.
У цьому випадку 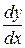 означає похідну неявної функції у, заданої рівнянням зв’язку
означає похідну неявної функції у, заданої рівнянням зв’язку 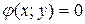 :
:
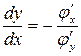 , тому
, тому 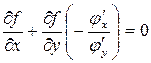 , тобто
, тобто 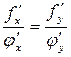 .
.
Позначивши останні відношення через 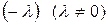 (знак “-“ взято для зручності) знайдемо, що в точці умовного екстремуму виконуються умови
(знак “-“ взято для зручності) знайдемо, що в точці умовного екстремуму виконуються умови 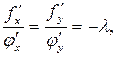 тобто
тобто
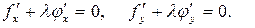
Отже стаціонарні точки умовного екстремуму мають задовольняти систему рівнянь
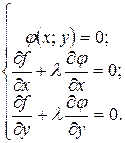 (1)
(1)
Аналізуючи цю систему, помічаємо, що знаходження умовного екстремуму функції 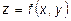 звелось до знаходження звичайного екстремуму функції
звелось до знаходження звичайного екстремуму функції
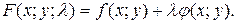 (2)
(2)
Функція (2) називається функцією Лагранжа, а число 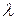 - множником Лагранжа.
- множником Лагранжа.
Умови (1) є лише необхідними. Вони дають змогу знайти стаціонарні точки умовного екстремуму. З теореми про достатні умови екстремуму випливає, що характер умовного екстремуму (достатні умови) можна встановити за знаком диференціала другого порядку функції Лагранжа: якщо в стаціонарній точці 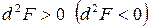 , то ця точка є точкою умовного мінімуму (максимуму).
, то ця точка є точкою умовного мінімуму (максимуму).
Для функції 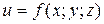 з рівняннями зв’язку
з рівняннями зв’язку 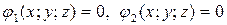 функція Лагранжа записується у вигляді
функція Лагранжа записується у вигляді 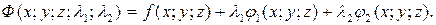
Стаціонарні точки умовного екстремуму знаходяться із системи рівнянь
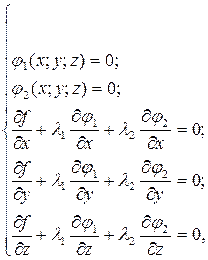
А достатні умови існування умовного екстремуму в цих точках можна визначити за знаком диференціала 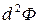 . Розглянутий метод можна поширити на дослідження умовного екстремуму функції довільного числа змінних.
. Розглянутий метод можна поширити на дослідження умовного екстремуму функції довільного числа змінних.
Задача 5.1. Найти область определения, а также частные похідні и дифференциал второго порядка функции 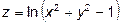 .
.
 2015-06-04
2015-06-04 1136
1136







