2015-06-04
230
Вариант 4.
2. Найдите все значения параметра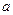 
, при каждом из которых уравнение 
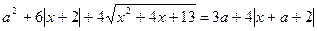имеет хотя бы один корень.
Решение:
1. Найдем область допустимых значений уравнения: выражение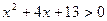 
для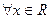 
, т. к. дискриминант D = - 36 < 0
2. Преобразуем данное уравнение к виду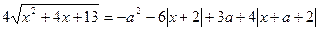 
.
Найдем наименьшее значение функции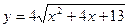 
Производная данной функции имеет вид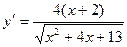 
x = - 2 – критическая точка. При x≤ - 2 функция 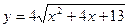убывает, при х≥ -2 функция неограниченно возрастает, т. к. производная 
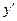< 0 при x ≤ - 2 и 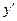> 0
при x ≥ - 2, т.е. x = - 2 – точка минимума.
Следовательно, функция 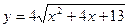на R принимает наименьшее значение в точке х=-2, y(-2)=12.
Таким образом, уравнение 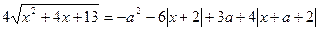имеет хотя бы один корень тогда и только тогда, когда функция f(-2) ≥ 12,
где f(x)=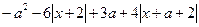 
f(-2) =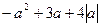 
Составим неравенство 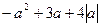≥ 12. Решением данного неравенства является совокупность:
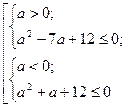
решением которой является отрезок [3;4].
Ответ: 3 ≤ а ≤ 4
Дана бесконечная арифметическая прогрессия, первый член которой равен 2012, а разность равна 5. Каждый член прогрессии заменили суммой его цифр. С полученной последовательностью поступили так же и действовали так до тех пор, пока не получилась последовательность однозначных чисел.
