Результаты опытов и их обработка. Заключение

Результаты восьми опытов вносим в таблицу 19.

Проверка однородности дисперсий проводится с целью принятия решения о возможности их использования для регрессионного анализа путем сравнения значений расчетного (G_p) и табличного (G_T) критериев Кохрена. Если G_T >G_P, то гипотеза об однородности дисперсии принимается.

Расчетное значение критерия Кохрена определяется по формуле:

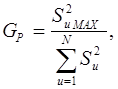(5)

где S_u² –дисперсия параллельных опытов,

N – количество опытов,

u – порядковый номер опыта.

Дисперсию параллельных опытов определяем по формуле:

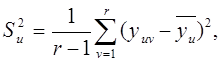(6)

где r – число параллельных опытов,

v – порядковый номер повторного опыта,

y_uv – значения параметров оптимизации в повторных опытах,

`y_u – среднеарифметическое значение параметров оптимизации.

Определим расчетное и табличное значение критерия Кохрена.

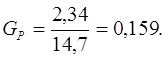
G_T выбираем из таблицы 7 [1] при числе степеней свободы f₁=r-1 и f₂=N, т.е. f₁=3-1 и f₂=8, и заданном уровне значимости p=0,05.

В нашем случае G_T=0,51. Так как G_T >G_P, гипотеза об однородности дисперсии принимается.

Таблица 19

Результаты испытаний и расчета дисперсий опытов

Номер опыта	Показатель фильтрации, см3/30 мин	`Yuv–Yu	(`Yuv–Yu)2	Su2
Yu1	Yu2	Yu3	`Yu	Yu1–`Yu	Yu2–`Yu	Yu3–`Yu	(Yu1–`Yu)2	(Yu2–`Yu)2	(Yu3–`Yu)2
				16,7	-1,7	+0,3	+1,3	2,89	0,09	1,69	2,34
					-1	+1
						-1	+1
				10,3	-0,3	+1,7	-1,3	0,09	2,89	1,69	2,34
						-1	+1
				9,3	-1,3	-0,3	+1,7	1,69	0,09	2,89	2,34
				8,7	-1,7	+0,3	+1,3	2,89	0,09	1,69	2,34
				6,3	-1,3	+1,7	-0,3	1,69	2,89	0,09	2,34
å	84,3		14,7

Коэффициенты уравнения регрессии рассчитаем по формулам 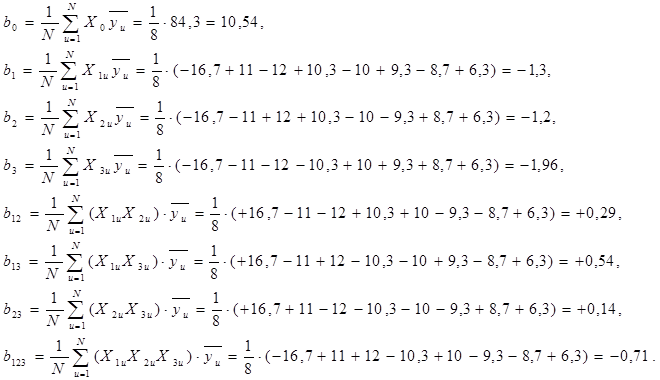После всех расчетов уравнение (4) примет вид:

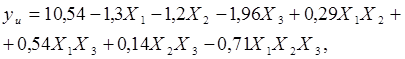(7)

Статистическая значимость коэффициентов уравнения (7) проверяется по условию b_i£2Db_i, где 2Db_i – доверительный интервал. Если это условие выполняется, то коэффициенты незначимы и члены уравнения (b_i) с незначимыми коэффициентами отбрасываются.

Граница доверительного интервала определяется по формуле:

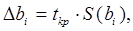
где t_kp – критическое значение критерия Стьюдента,

S(b_i) – средняя квадратичная ошибка коэффициентов уравнения регрессии.

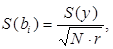
где S(y) – ошибка эксперимента,

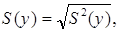
где S²(y) – дисперсия воспроизводимости, определяемая по формуле:

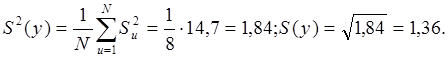
Для полнофакторного эксперимента ошибки всех коэффициентов равны между собой.

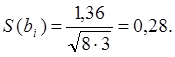
Критическое значение критерия Стьюдента выбирается по таблице 8 [1] в зависимости от числа степеней свободы f=8(3-1)=16 и заданного уровня значимости p=0,05 (t_kp=2,12).

Тогда: Db_i=2,12×0,28=0,59 и 2Db_i=1,18.

Следовательно, коэффициенты b₁₂, b₁₃, b₂₃, b₁₂₃ статистически не значимы и уравнение (7) примет вид:

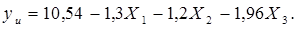(8)

Гипотеза об адекватности уравнения регрессии проверяется по условию: F_p£F_T, где

F_p,F_T – расчетное и табличное значения критерия Фишера.

Расчетное значение F_p определяется по формуле:

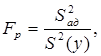
где S_ад² – дисперсия адекватности, определяемая по формуле:

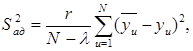(9)

где l – количество значимых коэффициентов уравнения регрессии,

`y_u – расчетное значение параметра оптимизации для каждого опыта.

Для составления таблицы 20 в уравнение (8) подставляем для каждого опыта значения X₁, X₂, X₃ из таблицы 18 и подсчитываем значения y_u.

Таблица 20

Расчетные и экспериментальные значения параметра оптимизации

Номер опыта	`Yu	Yu	`Yu –Yu	(`Yu –Yu)2
	16,7		+1,7	2,89
		12,4	-1,4	1,96
		12,6	-0,6	0,36
	10,3		-0,3	0,09
		11,08	-1,08	1,16
	9,3	8,48	+0,82	0,67
	8,7	8,68	+0,02	0,0004
	6,3	6,08	+0,22	0,048
å		7,1784

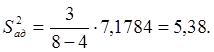
Определим расчетное значение критерия Фишера:

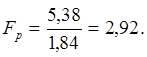
Табличное значение критерия Фишера определяется для соответствующих степеней свободы: f_ад=N-l; f_E=N(r-1) и принятого уровня значимости p=0,05 из таблицы 10 [1].

F_т=3,0 для f_ад=4; f_E=16. F_p <F_T=3,0, следовательно уравнения (7) и (8) адекватны.