Регулярные множества

Регулярные множества и регулярные выражения

В данном разделе мы рассмотрим класс множеств цепочек над конечным слова­рем, которые очень легко описать формулами некоторого вида. Эти множества называются регулярными.

Определение 1. Пусть V₁ и V₂ — множества цепочек. Определим три операции на этих множествах.

1. Объединение: V₁ ÈV₂ ={a| a Î V₁} или a Î V₂.

2. Конкатенация (произведение, склеивание): Vl ·V2 = {ab|a Î V₁,a Î V₂} Знак операции конкатенации обычно опускается.

Пример: V, = {abc, ba},V₂ = {b, cb}. V1V2 ={abcb, abccb, bab, bacb}.

Обозначим Vⁿ произведение n множеств V:Vⁿ =VV...V,V° ={e} (здесь e-пустая цепочка).

Пример: V₁ = {abc, ba}, V₁² = {abcabc, abcba, baba, baabc}.

3. Итерация: V* = V⁰ÈV¹ÈV² È... = È_a=0^∞Vⁿ.

Пример: V = {a, bc}, V* = {e, a, bc, aa, abc, bcbc, bca, aaa, aabc,...}.

Определение 4.13. Класс регулярных множеств над конечным словарем V определяется так:

1. 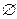— регулярное множество;

2. {e} — регулярное множество;

3. ("aÎV){a} — регулярное множество;

4. Если S и Т — регулярные множества, то регулярны:

- объединение SÈT;

- конкатенация ST;

- итерация S* и Т*.

5. Если множество не может быть построено конечным числом применения правил 1-4, то оно нерегулярно.

Примеры регулярных множеств: {ab, ba}* {aa}; {b}({c}È{d, ab}*). Примеры нерегулярных множеств: {aⁿbⁿ| n > 0}; {a | в цепочке a количества вхождений символов а и b совпадают}.