Это делает расчет сетевых структур более сложным, так как в данном случае определены другого рода задачи:
1. найти функцию распределения вероятности времени наступления события 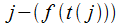 ;
;
2. определить вероятность того, что событие наступит не позднее момента 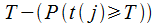 ;
;
3. найти функцию распределения критического пути 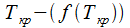 ;
;
4. найти среднее значение продолжительности критического пути — 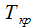 ;
;
5. определить наименьшее и наибольшее значения продолжительности критического пути — 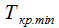 и
и 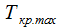 ;
;
6. вычислить вероятность реализации совокупности работ за плановое время 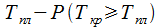 и т.п.
и т.п.
В качестве начальных данных для таких расчетов представляются закономерности распределения продолжительности отдельных сетевых работ.
Статистические исследования показали, что продолжительность 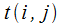 для большинства распространенных типов работ описывается
для большинства распространенных типов работ описывается 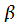 -распределением (рис. 6.21, б):
-распределением (рис. 6.21, б):
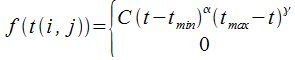
при 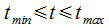 ; в иных случаях.
; в иных случаях.
В данном случае 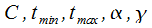 представлены в качестве констант, при этом
представлены в качестве констант, при этом 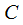 находится из условия нормирования:
находится из условия нормирования:
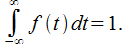
Константы 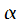 и
и 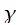 предполагают зависимость от специфики работ (рис. 6.21, б — в данном случае
предполагают зависимость от специфики работ (рис. 6.21, б — в данном случае 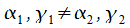 ).
).
|
|
|
Бета-распределение является одним из самых распространенных в математической
статистике. Его специальными случаями являются F-распределение, закон арксинуса.
Бета-распределение связано с гамма-распределением, равномерным и биноминальным распределениями [1].
Плотность бета-распределения плотности вероятностей ущерба распределяется по следующему закону [1]:
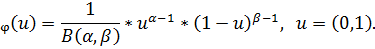
где В(α,β) -бета-функция, которая имеет вид:
В(α,β) = Г(α)-Г(β)/Г(α + β).
Здесь Г(а) - гамма-функция (принимает табличные значения), а>0ир>0 - свободные параметры гамма-функции. Интегральная функция распределения определяется выражением [1]:
Ф(U) = 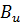 (α,β)/В(α,β),
(α,β)/В(α,β),
где 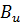 (α,β)- неполная бета-функция, которая принимает табличные значения и находится с помощью интеграла
(α,β)- неполная бета-функция, которая принимает табличные значения и находится с помощью интеграла
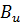 (α,β)=
(α,β)= 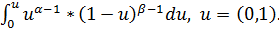
Вероятность превышения значения порогового ущерба U2, который является макcимально допустимым, находится по формуле
P(u≤u2) = Ф(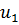 )=
)= 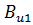 (α, β) / В(α, β).
(α, β) / В(α, β).
Вероятность попадания причиненного ущерба в заданный интервал [щ, U2] является площадью под кривой плотности распределения и находится как разность двух инте гральных функций распределения
P(u≥u2)=1-1 - Ф(u2) = 1 - 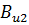 (α, β) / В(α, β).
(α, β) / В(α, β).
Таблица интегральных, усредненных рисков и защищенности для непрерывного бета распределения вероятностей ущерба
| Вид риска и защищенности | Аналитическое выражение |
| Risk(u≤u2) | 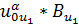 (α, β)* [ 1 - (α, β)* [ 1 - 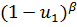 ]/(β * [B(α, β)]2) ]/(β * [B(α, β)]2)
|
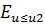
| β * [B(α,β)]2 /«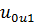 * Bu (α,β).[1 - * Bu (α,β).[1 - 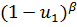 - ]) - ])  1 1
|
| Risk(u1≤u≤u2) | 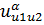 *[B (α, β)*- *[B (α, β)*- 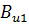 (α, β)]- [ (α, β)]- [ 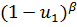 - - 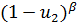 ]/(β • [B(α, β)]2 ]/(β • [B(α, β)]2
|
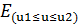
| 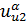 * [B (α, β)] /[ * [B (α, β)] /[ 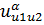 * B (α,β)- * B (α,β)- 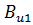 ( (α,β)]- [ ( (α,β)]- [ 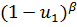 - - 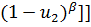 -1 -1
|
| Risk(u≤u2) | 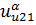 * [B(α, β) – Bu2 (α, β)]- * [B(α, β) – Bu2 (α, β)]- 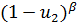 ]/(β •*[B(α, β)]2] ]/(β •*[B(α, β)]2]
|
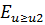
| 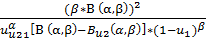 -1 -1
|
Risk(u 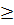 u2) u2)
| 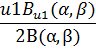
|
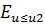
| 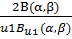 -1 -1
|
| Risk(u1≤u≤u2) | 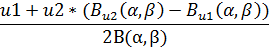
|
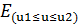
| 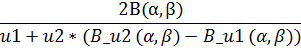
|
Risk(u  u2) u2)
| 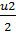 [1- [1- 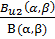 ] ]
|
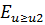
| 2 • B(α,β)/(u2 • [B(α,β) - 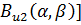 ) -1 ) -1
|
Следует отметить, что полученные интегральные риски являются не функциями, а константами (числами), характеризующими ущерб в некотором интервале.
|
|
|
Элементарный риск определяется с помощью дискретизации плотности бета –распределения. Рассмотрим отрезок [0;umax], где umax - значение максимально допустимого ущерба. Превышение значения umax означает “смерть” системы. Вероятность превышения umax:
Р(u 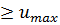 ) =1-
) =1- 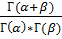 *
* 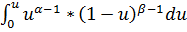 =1-
=1- 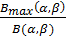 .
.
Разобьем полученный отрезок на n дискрет 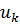 . Период дискретизации ∆u, к - дискретная переменная, k={
. Период дискретизации ∆u, к - дискретная переменная, k={ 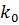 ,
, 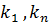 }. Пронормировав по
}. Пронормировав по 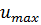 = n*∆u, получим получим единичное пространство.
= n*∆u, получим получим единичное пространство.
Risk( )=
)= 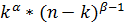 /
/ 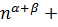 B(α,β)).
B(α,β)).
Тогда защищенность системы можно определить выражением
E= 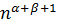 * B(α,β)/
* B(α,β)/ 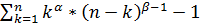 .
.
Как видно из вышеприведенной формулы, на состояние защищенности влияют параметры бета-распределения вероятностей ущерба а, Р и количество выборок, получаемых при дискретизации плотности бета распределения.
Рассмотрим функцию элементарного риска и определим ее параметры: матожидание 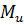 , дисперсию D, среднее квадратическое отклонение Ϭ, коэффициент вариации v, коэффициент асимметрии As, коэффициент эксцесса
, дисперсию D, среднее квадратическое отклонение Ϭ, коэффициент вариации v, коэффициент асимметрии As, коэффициент эксцесса 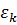 , моду
, моду 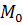 , медиану
, медиану 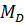 , производные первого и второго порядков риска,точку максимума
, производные первого и второго порядков риска,точку максимума 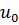 , точки перегиба
, точки перегиба 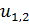 , начальные
, начальные 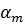 и центральные
и центральные 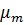 моменты, размах варьирования R представлены в табл. 2
моменты, размах варьирования R представлены в табл. 2
| Вид параметра | Аналитическое выражение |
Risk( ) )
| 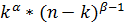 / / 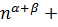 B(α,β)) B(α,β))
|
| E | 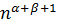 * B(α,β)/ * B(α,β)/ 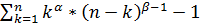
|
| risk’(u) | 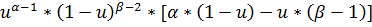
|
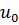
| α/[α+β-1] |
| risk"(u) | 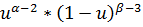 *[ *[ 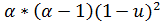 -2 -2 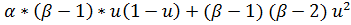
|
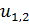
| 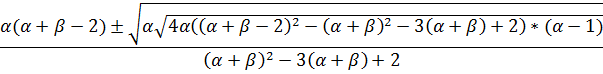
|
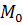
| α/(α+β-1) |
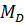
| 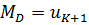 ,n=2*k+1; ,n=2*k+1; 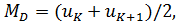 n=2*k n=2*k
|
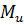
| 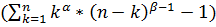 / / 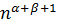 * B(α,β) * B(α,β)
|
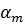
| 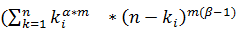 / / 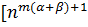 *[ *[ 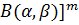 ] ]
|
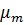
| 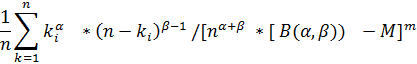
|
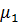
| |
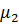
| D(u) |
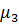
| 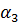 - - 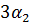 * * 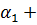 2 2 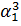
|
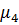
| 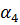 -4 -4 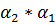 +6 +6 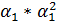 -3* -3* 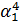
|
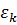
| 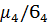 -3 -3
|
| D | 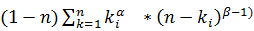 / / 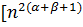 *[ *[ 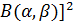 ] ]
|
| Ϭ | 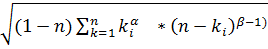 / / 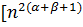 *[ *[ 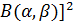 ] ]
|
| v | 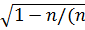 * * 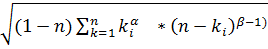
|
| R | α/(α+β-1)- 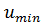
|
 2015-06-04
2015-06-04 319
319






