| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника | 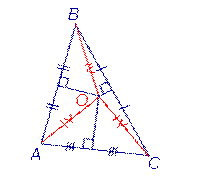 | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника | 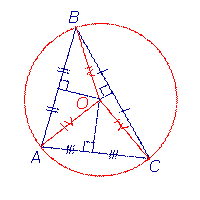 | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности | 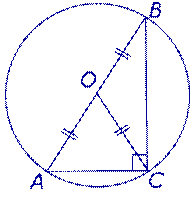 | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности | 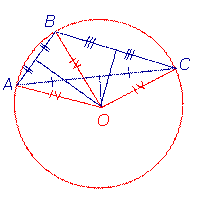 | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов | 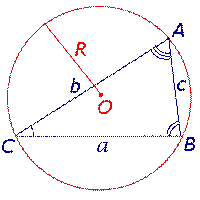 | Для любого треугольника справедливы равенства (теорема синусов): 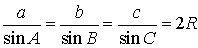 , где a, b, c – стороны треугольника, A, B, С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника | 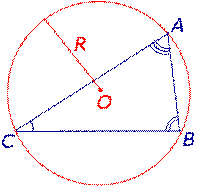 | Для любого треугольника справедливо равенство: S = 2 R 2 sin A sin B sin C, где A, B, С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности | | Для любого треугольника справедливо равенство: 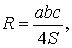 где a, b, c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
Свойства описанной около треугольника окружности. Теорема синусов
2015-06-04
1659Поделись с друзьями:
|
|
Сейчас читают про:
8259
8174