Дати означення ф-ції розподілу імовірностей с.в.в. Сформулювати її основні властивості та геометричний зміст.
Случайные величины, возможные значения которых определяются одним числом наз одномерными. Величины, возможные значения которых определяются двумя, тремя, …, n числами наз соответственно двумерными, трёхмерными, …, n-мерными.
Будем обозначать через (X,Y) двумерную с.в. Каждую из величин X и Y наз составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Ф-ция распределения двумерной с.в.
Рассмотрим двумерную с.в. (X,Y) (безразлично, дискретную или непрерывную). Пусть x,y – пара действительных чисел. Вероятность события, состоящего в том, что X примет значение, меньшее x, и при этом Y примет значение, меньшее y, обозначим через F(x,y). Если x и y будут изменяться, то будет изменяться и F(x,y), т.е. F(x,y) есть ф-ция от x и y.
Ф-цией распределения двумерной с.в. (X,Y) наз ф-цию F(x,y), определяющую для каждой пары чисел x,y вероятность того, что X примет значение, меньшее x, и при этом Y примет значение, меньшее y:
F(x,y)=P(X< x, Y< y)
Геометрически это равенство можно истолковать так: F(x,y) есть вероятность того, что случайная точка (X,Y) попадет в бесконечный квадрат с вершиной (x,y), расположенный левее и ниже этой вершины (с.158 Гмурман)
Свойство1. Значения ф-ции распределения удовлетворяют двойному неравенству
0≤F(x,y)≤1
Свойство2. F(x,y) есть неубывающая ф-ция по каждому аргументу, т.е.
F(x2,y)≥ F(x,y), если x2>x1
F(x,y2)≥ F(x,y), если y2>y1
Свойство3. Имеют место предельные соотношения:
1) F(-∞, y)=0 3) F(-∞,-∞)=0
2) F(x, -∞)=0 4) F(∞, ∞)=1
Свойство4.
а) При y=∞ ф-ция распределения системы становится ф-цией распределения составляющей X:
F(x, ∞)=F1(x)
б) При x=∞ ф-ция распределения системы становится ф-цией распределения составляющей Y:
F(∞, y)=F2(y)
26. Пояснити, як будуються випадкові величини, що мають розподіл: а) Пірсона χ2 (χ2-розподіл), б) Стьюдента (t-розподіл), в) Фішера (F-розподіл). Записати вирази для ф-ції щільності розподілу імовірностей цих розподілів та їх основні числові характеристики. Пояснити зміст позначень.
а) Пусть Xi(i=1,2,…,n) – нормальные независимые случайные величины, причем мат. ож-ние каждой из них равно нулю, а среднее квадратическое отклонение – единице. Тогда сумма квадратов этих величин 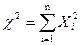 распределена по закону χ2 («хи квадрат») с k=n степенями свободы; если же эти величины связаны одним линейным соотношением, например
распределена по закону χ2 («хи квадрат») с k=n степенями свободы; если же эти величины связаны одним линейным соотношением, например 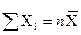 , то число степенем свободы k=n-1.
, то число степенем свободы k=n-1.
Плотность этого распределения
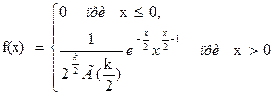 ,
,
где 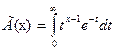 - гамма-функция; в частности, Г(n+1)=n!
- гамма-функция; в частности, Г(n+1)=n!
б) Пусть Z – нормальная случайная величина, причем M(Z)=0, σ(Z)=1, а V – независимая от Z величина, которая распределена по закону χ2 с k степенями свободы. Тогда величина
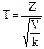 имеет распределение, которое наз t-распределением или распределением
имеет распределение, которое наз t-распределением или распределением  Стьюдента с k степенями свободы.
Стьюдента с k степенями свободы.
в) Если U и V – независимые случайные величины, распределенные по закону χ2 со степенями свободы k1 и k2, то величина 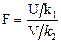 имеет распределение, которое наз распределением F Фишера-Снедекора со степенями свободы k1 и k2 (иногда его обозначают через V2).
имеет распределение, которое наз распределением F Фишера-Снедекора со степенями свободы k1 и k2 (иногда его обозначают через V2).
Плотность этого распределения
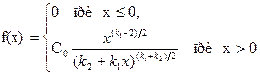
где 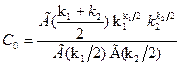




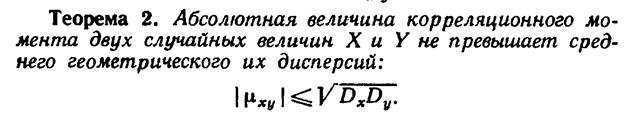

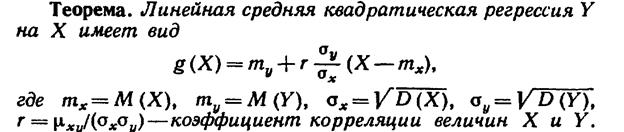





 15.
15.


В) Досить часто для характеристики зв’язку між випадковими величинами 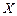 і
і 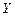 використовують коефіцієнт кореляції
використовують коефіцієнт кореляції
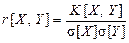 .
.
Коефіцієнт кореляції характеризує тільки зв'язок між випадковими величинами, тоді як 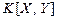 крім зв’язку між випадковими величинами
крім зв’язку між випадковими величинами 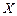 і
і 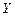 характеризує ще й величину розсіювання. Коефіцієнт кореляції є безрозмірною величиною.
характеризує ще й величину розсіювання. Коефіцієнт кореляції є безрозмірною величиною.
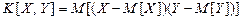 можна розглядати як скалярний добуток величин
можна розглядати як скалярний добуток величин 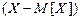 і
і 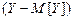 .
. дістаємо так званий умовний дискретний розподіл імовірностей випадкової величини 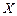 за умови, що випадкова величина
за умови, що випадкова величина 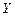 набуває значення
набуває значення 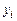 ,
, 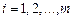 . Числа
. Числа 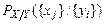 ,
, 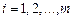 ,
, 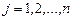 , можна тлумачити як значення деякої випадкової величини
, можна тлумачити як значення деякої випадкової величини 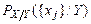 ,
, 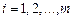 , яких вона набуває з імовірностями
, яких вона набуває з імовірностями 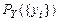 ,
,
Нехай 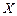 – дискретна випадкова величина, що набуває значень
– дискретна випадкова величина, що набуває значень 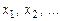 , тобто
, тобто
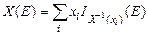 .
.
Нехай 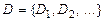 – деяке розбиття.
– деяке розбиття.
Умовним математичним сподіванням випадкової величини 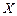 щодо розбиття
щодо розбиття 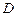 називають випадкову величину
називають випадкову величину
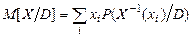 ,
, 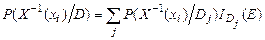 .
.
Якщо при цьому 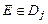 , то
, то 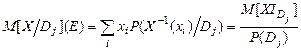 ,
,
тобто для 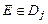 випадкова величина
випадкова величина 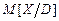 набуває одного й того самого значення
набуває одного й того самого значення 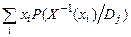 .
.
Якщо 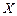 – довільна випадкова величина, для якої визначено
– довільна випадкова величина, для якої визначено 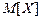 ,
, 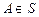 – випадкова подія така, що
– випадкова подія така, що 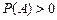 , то величину
, то величину
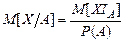 ,
, 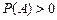 ,
,
називають умовним математичним сподіванням випадкової величини 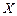 щодо події
щодо події 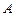 .
.
Г) Узагальненими числовими характеристиками випадкових величин є початкові та центральні моменти.
ОЗНАЧЕННЯ 5.8. Початковим моментом k-го порядку випадкової величини x називають математичне сподівання величини xk:
ak = ak(x) = М(xk) (k = 1,2,3, …).
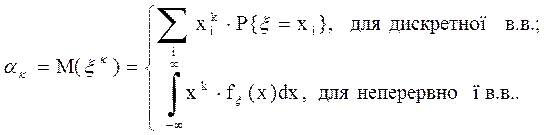
|
ОЗНАЧЕННЯ 5.9. Центральним моментом k-го порядку випадкової величини x називають математичне сподівання від величини (x - Мx)k:
mk = mk(x) = М(x-Мx)k (k = 1,2,3, …).
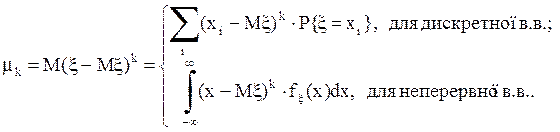
|
Відзначимо кілька важливих положень:
- Число М½x½k називають абсолютним початковиммоментом порядку k випадкової величини x;
- Число М½x - Мx½k називають абсолютним центральним моментом порядку k випадкової величини x;
- З означень 5.8 та 5.9 маємо, що коли існують моменти Мxk, то існують й моменти менших порядків.
- Вірні наступні порівняння:
а) a = m = 1;
б) Mx = a1;
в) Dx = s2x = m2 = a2 - a12;
г) m1 = 0.
Як ми бачимо, другий центральний момент (в): m2 - дисперсіявипадкової величини.
Зауважимо ще те, що центральні моменти mk можна обчислити через начальні моменти a1, a2, …, ak.
Чим більш моментів випадкової величини відомі, тим детальніше уявлення про закон розподілу. В теорії ймовірностей та її застосуванні використовують ще дві числові характеристики випадкової величини, які обчислюються за допомогою третього та четвертого моментів.
Б) Вибіркові дисперсії s 2, S 2 — це числові характеристики розсіювання значень випадкової вибірки, що являє собою сукупність результатів незалежних повторних спостережень. Визначаються в звичайних сукупностях вимірів. В теорії точності вимірювань їх ще називають дисперсіями вимірів, або просто дисперсіями.
- Дисперсія s 2 — це різниця середнього значення
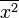 квадратів елементів вибірки і квадрата
квадратів елементів вибірки і квадрата 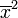 вибіркового середнього:[3]
вибіркового середнього:[3]
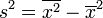 .
.
- Дисперсія S 2 є різниця середнього значення
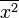 квадратів елементів вибірки і середнього значення
квадратів елементів вибірки і середнього значення 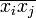 добутку двох її елементів:
добутку двох її елементів:
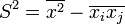 .
.
- Вибіркові дисперсії мають такий вигляд:
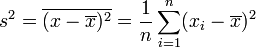 ;
; 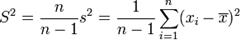
 2015-06-16
2015-06-16 370
370






