Свойства сумм Дарбу

Вопрос №30

Определение

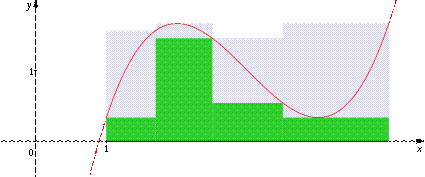
Нижняя (зеленая) и верхняя (серая) суммы Дарбу на 4 отрезках разбиения

Пусть на отрезке 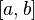определена вещественнозначная функция 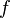. Рассмотрим разбиение

.

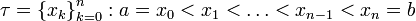Введем обозначения

,

.

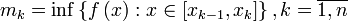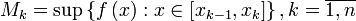Наконец, рассмотрим суммы

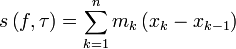– нижняя сумма Дарбу,

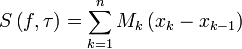- верхняя сумма Дарбу.

Свойства сумм Дарбу

• Нижняя сумма Дарбу не превосходит верхней суммы Дарбу на заданном разбиении.

;

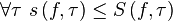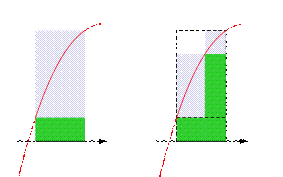
Поведение нижней (зеленая) и верхней (серая) сумм Дарбу на измельчении разбиения --При добавлении к имеющемуся разбиению новых точек, нижняя сумма Дарбу никак не может уменьшиться. Верхняя сумма Дарбу же при добавлении точек к имеющемуся разбиению никак не может увеличиться.

,

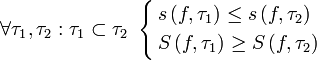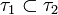означает, что 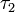есть измельчение разбиения ;

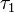• Каковы бы ни были два разбиения одного и того же отрезка, нижняя сумма Дарбу на одном разбиении не превосходит верхней суммы Дарбу на другом разбиении.

,

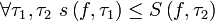Следствие: нижние суммы Дарбу ограничены сверху, а верхние - снизу.

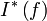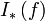• Пусть и – верхний и нижний интегралы Дарбу соответственно. Тогда

;

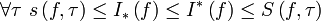• Пусть 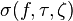— интегральная сумма. Тогда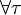

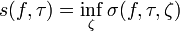
• При увеличении количества точек разбиения верхняя сумма не увеличивается, а нижняя не уменьшается.

Интеграл Дарбу[править | править вики-текст]

Верхним интегралом Дарбу называют число

,

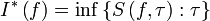где 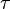— некоторое разбиение множества, а 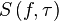— его верхняя сумма Дарбу.

Соответственно нижним интегралом Дарбу называют:

,

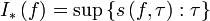где 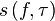— нижняя сумма Дарбу.

Критерий Дарбу интегрируемости функции[править | править вики-текст]

Приведенные утверждения даны для функции одной переменной.

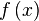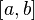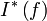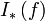Пусть вещественнозначная функция определена и ограничена на отрезке . Пусть и - верхний и нижний интегралы Дарбу функции 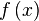на заданном отрезке соответственно. Тогда следующие 3 условия эквивалентны:

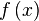• интегрируема по Риману на отрезке , ,
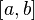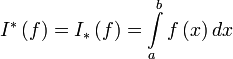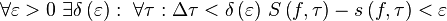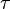• , где и 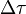— некоторое разбиение и его мелкость.