
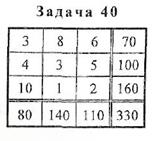
Решение. Составляем начальную транспортную таблицу с нулевыми перевозками.
| Поставщик | Потребитель | Запасы груза | |||||||||||
| B1 | B2 | B3 | |||||||||||
| A1 | |||||||||||||
| A2 | |||||||||||||
| A3 | |||||||||||||
| Потребность |
Транспортная задача имеет закрытый тип, так как суммарный запас груза
70+100+160=330
равен суммарным потребностям
80+140+110=330.
Найдем опорный план по методу минимального тарифа.
Находим незанятую клетку с минимальным тарифом: (3,2). Помещаем туда меньшее из чисел 160 и 140.
Находим незанятую клетку с минимальным тарифом: (3,3). Помещаем туда меньшее из чисел 20 и 110.
Находим незанятую клетку с минимальным тарифом: (1,1). Помещаем туда меньшее из чисел 70 и 80.
Находим незанятую клетку с минимальным тарифом: (2,1). Помещаем туда меньшее из чисел 100 и 10.
Находим незанятую клетку с минимальным тарифом: (2,3). Помещаем туда меньшее из чисел 90 и 90.
Получили:
| Поставщик | Потребитель | Запасы груза | |||||||||||
| B1 | B2 | B3 | |||||||||||
| A1 | |||||||||||||
| A2 | |||||||||||||
| A3 | |||||||||||||
| Потребность |
Стоимость перевозок по этому плану равна:
F = 70*3+10*4+90*5+140*1+20*2 = 880.
Будем решать задачу методом потенциалов. Проверяем найденный план на оптимальность. Полагая потенциал U1=0, определяем остальные потенциалы из соотношения Ui+Vj=Ci,j, просматривая все занятые клетки.
Потенциалы:
U1=0
V1=C1,1-U1= 3
U2=C2,1-V1=1
V3=C2,3-U2= 4
U3=C3,3-V3=-2
V2=C3,2-U3= 3
Определяем значения оценок Si,j=Ci,j-(Ui+Vj) для всех свободных клеток:
S1,2 = C1,2 - (U1 + V2) = 5.
S1,3 = C1,3 - (U1 + V3) = 2.
S2,2 = C2,2 - (U2 + V2) = -1.
S3,1 = C3,1 - (U3 + V1) = 9.
Выбираем клетку (2,2) с отрицательной оценкой -1. Строим для нее цикл, помечая клетки цикла знаками "плюс" и "минус".
 Поставщик Поставщик
| Потребитель | Запасы груза | |||||||||||
| B1 | B2 | B3 | |||||||||||
| A1 | |||||||||||||
| A2 |
|
| |||||||||||
| A3 |
|
| |||||||||||
| Потребность |
Перемещаем по циклу груз величиной в 90 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус".
В результате перемещения по циклу получим новый план:
| Поставщик | Потребитель | Запасы груза | |||||||||||
| B1 | B2 | B3 | |||||||||||
| A1 | |||||||||||||
| A2 | |||||||||||||
| A3 | |||||||||||||
| Потребность |
Стоимость перевозок F = 70*3+10*4+90*3+50*1+110*2=790.
Проверяем найденный план на оптимальность. Полагая потенциал U1=0, определяем остальные потенциалы из соотношения Ui+Vj=Ci,j, просматривая все занятые клетки.
Потенциалы:
U1=0
V1=C1,1-U1= 3
U2=C2,1-V1=1
V2=C2,2-U2= 2
U3=C3,2-V2=-1
V3=C3,3-U3= 3
Определяем значения оценок Si,j=Ci,j-(Ui+Vj) для всех свободных клеток:
S1,2 = C1,2 - (U1 + V2) = 6.
S1,3 = C1,3 - (U1 + V3) = 3.
S2,3 = C2,3 - (U2 + V3) = 1.
S3,1 = C3,1 - (U3 + V1) = 8.
Так как все оценки положительны, то полученный план является оптимальным.
Транспортная задача решена. Минимальная стоимость перевозок равна 790.
План перевозок:
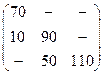
Задача 70. Найти решение и цену игры, заданной следующей платежной матрицей:
Решение. Попробуем найти седловую точку данной платежной матрицы.
Найдем наилучшую стратегию первого игрока: минимальное число в каждой строке обозначим 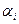 . Получаем:
. Получаем: 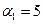 ,
, 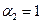 . Выберем максимальное из этих значений
. Выберем максимальное из этих значений 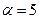 - нижняя цена игры, стратегия А1.
- нижняя цена игры, стратегия А1.
Аналогично для второго игрока. Найдем максимальные значения выигрыша по столбцам: 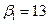 ,
, 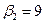 и минимальное из этих чисел
и минимальное из этих чисел 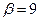 - верхняя цена игры, стратегия В2.
- верхняя цена игры, стратегия В2.
Так как верхняя и нижняя цены игры различны, игра не имеет решения в чистых стратегиях (седловой точки нет), цена игры находится в промежутке от 5 до 9 (между нижней и верхней ценой игры).
Решим данную игру аналитическим методом.
Средний выигрыш первого игрока, если он использует оптимальную смешанную стратегию 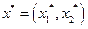 , а второй игрок – чистую стратегию, соответствующую первому столбцу платежной матрицы, равен цене игры
, а второй игрок – чистую стратегию, соответствующую первому столбцу платежной матрицы, равен цене игры 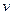 :
:
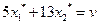 .
.
Тот же средний выигрыш получает первый игрок, если второй игрок применяет стратегию, соответствующую второму столбцу платежной матрицы, то есть
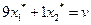 .
.
Учитывая, что 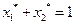 , получаем систему уравнений для определения оптимальной стратегии первого игрока и цены игры:
, получаем систему уравнений для определения оптимальной стратегии первого игрока и цены игры:
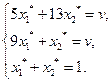
Решаем эту систему и находим:
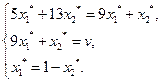
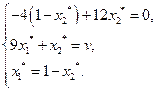
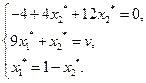
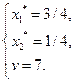
Применяя теорему об активных стратегиях при отыскании смешанной стратегии второго игрока, получаем, что при любой чистой стратегии первого игрока средний проигрыш второго игрока равен цене игры, то есть:
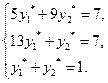
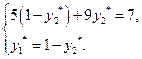
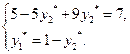
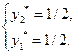
Отсюда находим 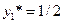 ,
, 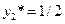 .
.
Игра решена. Оптимальные смешанные стратегии 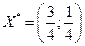 ,
, 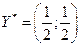 , цена игры
, цена игры 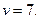
 2015-06-16
2015-06-16 271
271
 140
140







