3.1. Определение тройного интеграла
Тройной интеграл является полным аналогом двойного интеграла. Пусть в некоторой трёхмерной области (V) задана непрерывная функция трёх переменных 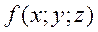 .
.
Разобьём область (V) произвольным образом на n элементарных областей (Vi)(i=1,2…n) без общих внутренних точек, объёмы которых обозначим через 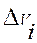 .
.
Выберем в каждой части произвольную точку 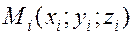 и составим интегральную сумму
и составим интегральную сумму
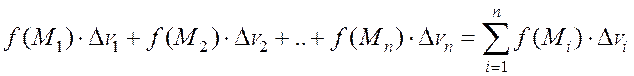
Обозначим через λ наибольший из диаметров элементарных областей(V1), (V2)…. (Vn): 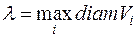 , где
, где 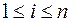 .
.
Если существует предел интегральной суммы 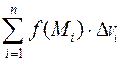 при λ→0 (n→∞), не зависящий ни от способа разбиения области(V) наэлементарные области, ни от выбора точек
при λ→0 (n→∞), не зависящий ни от способа разбиения области(V) наэлементарные области, ни от выбора точек 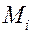 в каждой элементарной области, то этот предел называют тройным интегралом от функции
в каждой элементарной области, то этот предел называют тройным интегралом от функции 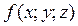 по области (V) и обозначают:
по области (V) и обозначают:
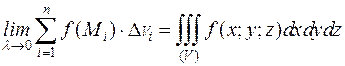
Функция 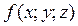 в этом случае называется интегрируемой в области (V).
в этом случае называется интегрируемой в области (V).
Замечание. Свойства тройных интегралов полностью аналогичны свойствам двойных интегралов.
3.2. Вычисление тройных интегралов
3.2.1. Вычисление тройного интеграла в прямоугольных координатах
Пусть 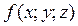 – непрерывная в области (V) функция, (V) – часть пространства ограниченная сверху поверхностью
– непрерывная в области (V) функция, (V) – часть пространства ограниченная сверху поверхностью 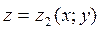 , а снизу – поверхностью
, а снизу – поверхностью 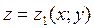 .
.
Пусть (D) – проекция области (V) на плоскость Oxy.
Границей области (D) «сверху» является график функции 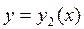 , «снизу» - график функции
, «снизу» - график функции 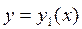 .
.
Проекцией области (D) на ось Ox является отрезок [ a;b ] (рис. 14)
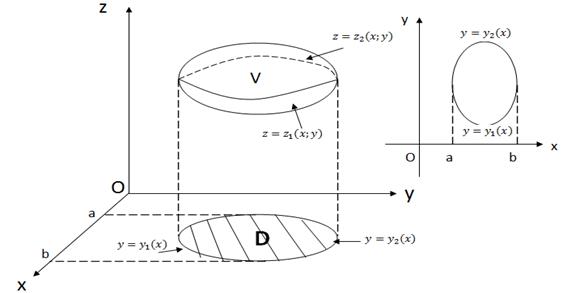
Рис. 14
Тогда имеет место формула:
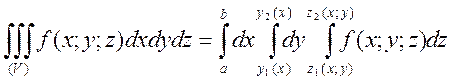
Пример
Вычислить 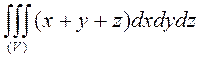 ,
,
если (V) – область, ограниченная плоскостями x=0, y=0, z=0, x+y+z=1.
Решение Область (V) изображена на рисунке (15). Поэтому

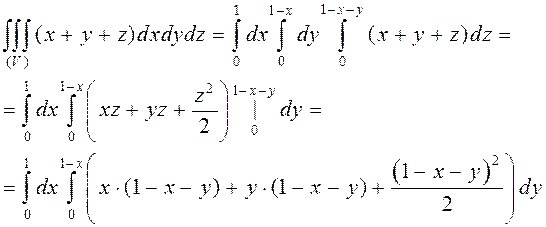
Путем несложных вычислений можно придти к ответу 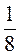 .
.
Замечание. Если 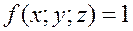 , то
, то
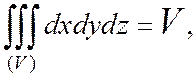
где 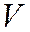 – объём области (V).
– объём области (V).
3.2.2. Тройной интеграл в цилиндрических координатах.
В цилиндрической системе координат положение точки M пространства определяется полярными координатами r и 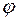 точки
точки 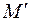 – проекции точки M на плоскость Oxy и аппликатой z самой точки M,то есть
– проекции точки M на плоскость Oxy и аппликатой z самой точки M,то есть 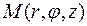 (рис. 15).
(рис. 15).
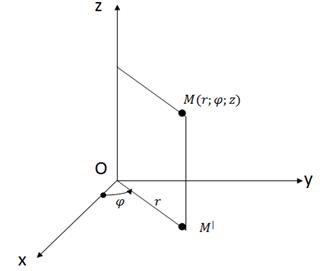
Рис. 15
Числа r, φ, z называют цилиндрическими координатами точки M.
При этом 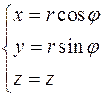 ,
, 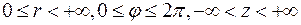
При переходе к цилиндрической системе координат элемент объема равен 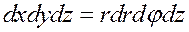 , r -якобиан перехода.
, r -якобиан перехода.
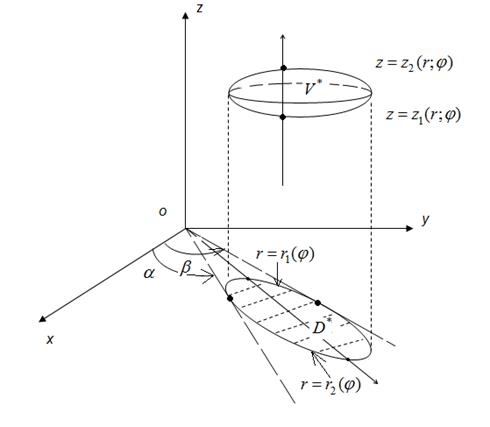
Рис.16
Тогда справедлива формула
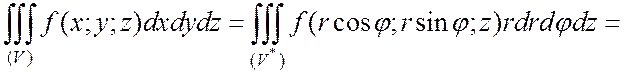
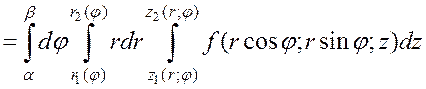 .
.
Пример Найти объём цилиндра высотой H и радиусом основания R.
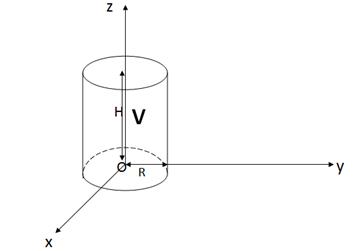 Решение Изобразим данный цилиндр в системе координат Oxyz (рис. 17).
Решение Изобразим данный цилиндр в системе координат Oxyz (рис. 17).
Рис. 17
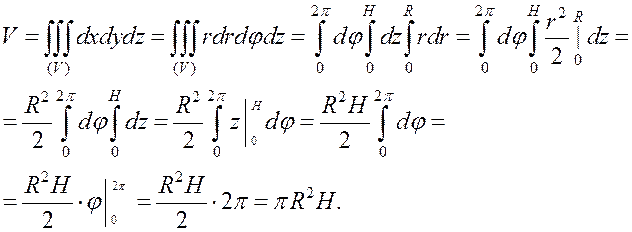
3.2.3. Тройной интеграл в сферических координатах.
В сферической системе координат положение точки M в пространстве определяется расстоянием r от точки M до начала системы координат, полярным углом φ между положительным направлением оси Ox и проекцией радиус-вектора 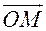 точки M на плоскость Oxy и углом θ между положительным направлением оси Oz и радиус-вектором
точки M на плоскость Oxy и углом θ между положительным направлением оси Oz и радиус-вектором 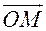 точки M (рис. 18).
точки M (рис. 18).
Числа r, φ, θ называют сферическими координатами точки M.
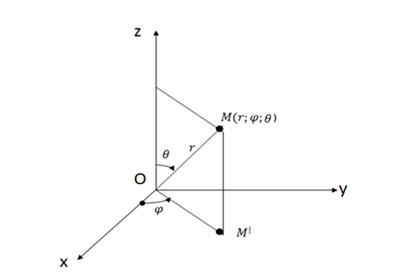
Рис. 18
При этом
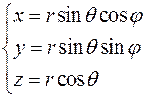 ,
, 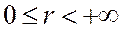 ,
, 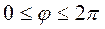 ,
, 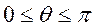 .
.
При переходе к цилиндрической системе координат элемент объёма равен 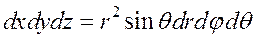 ,
, 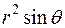 -якобиан перехода.
-якобиан перехода.
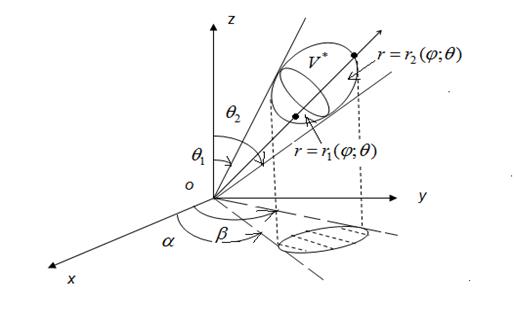
Рис.19
Тогда справедлива формула:
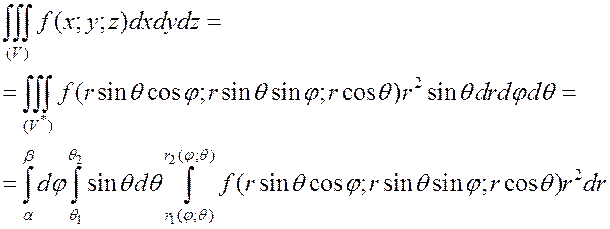
Пример Найти объём шара радиуса R.
Решение Изобразим шар в системе координат Oxyz (рис. 20).
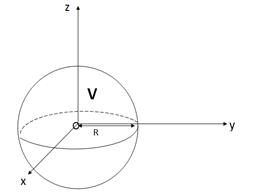 |
Рис. 20
Тогда

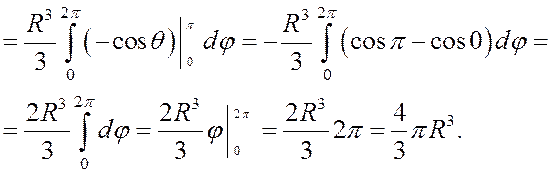
 2015-06-04
2015-06-04 6332
6332