Базис системы векторов

Дана система векторов (конечная или бесконечная). Совокупность n - мерных векторов, 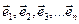называется базисом (системой координат) векторного пространства Rⁿ, если они линейно независимы и любой вектор этого пространства является линейной комбинацией. 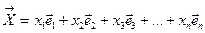(3.2.2)

Равенство (3.2.2) называется разложением вектора 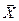по базису 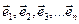, а компоненты вектора x_1,x₂,x₃,…x_n называются его координатами в этом базисе.

Имеют место утверждения:

1. Каждый вектор системы может быть разложен по базису единственным способом.

2. Два различных базиса одной и той же системы векторов содержат одинаковое количество векторов.

3. Система n -линейно независимых векторов 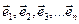образует базис в пространстве Rⁿ

4. В пространстве Rⁿ система, состоящая более чем из n векторов, линейно зависима.