Теоретическая часть. Основными силами взаимодействия -частиц с веществом являются кулоновские силы, основными процессами взаимодействия - процессы упругого рассеяния и

Основными силами взаимодействия -частиц с веществом являются кулоновские силы, основными процессами взаимодействия - процессы упругого рассеяния и ионизационного торможения.

Упругое рассеяние - такой процесс взаимодействия двух частиц, при котором суммарная кинетическая энергия обеих частиц сохраняется и происходит лишь перераспределение ее между частицами. При этом сами частицы изменяют направление своего движения, т. с. происходит процесс рассеяния.

Проходя через вещество, - частицы почти не рассеиваются на электронах среды из-за своей большой массы (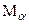 = 7350 m_е, в результате столкновения с электроном они отклоняются от первоначального направления не более чем на 30"). Столкновения с ядрами, напротив, приводят к их значительному рассеянию.

Упругое рассеяние заряженной частицы на тяжелом ядре описывается формулой Резерфорда

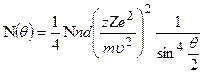, (1.1)

где N(θ) — число частиц, рассеянных в единице телесного угла под углом θ; N - число частиц, падающих на 1 см² мишени в 1 с; п — число ядер в 1 см³; d — толщина мишени; Z заряд ядра-рассеивателя; z, т и 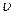— заряд, масса и скорость частицы.

Формула Резерфорда была проверена экспериментально и оказалось, что она хорошо согласуется с опытом для широкого диапазона рассеивающих ядер, углов рассеяния и скоростей -частиц.

Вывод формулы (1.1) был основан на следующих предположениях:

1. Между частицей и ядром действуют только кулоновские силы. В действительности помимо кулоновских сил между частицей и ядром при малых прицельных параметрах (большие углы рассеяния) могут действовать ядерные силы. Опыты по изучению рассеяния -частиц больших энергий на ядрах показали, что существуют отступления от формулы Резерфорда, и характер этих отступлений позволил сделать определенные заключения о некоторых особенностях ядерных сил.

2. Отсутствует экранирование ядра атомными электронами. Между тем экранирование является существенным для малых углов рассеяния, когда частица пролетает на больших расстояниях от ядра. Поэтому для очень малых углов рассеяния формула (1.1) должна быть уточнена.

3. Масса налетающей частицы значительно меньше массы ядра. В этом случае частица при столкновении с ядром практически не теряет энергии, а лишь меняет направление движения (ядро остается неподвижным).

4. Скорость налетающей частицы значительно меньше скорости света (частица нерелятивистская).

5. Спины налетающей частицы и ядра - мишени равны нулю.

Формулы, учитывающие указанные эффекты, выведены Моттом. Они хорошо подтверждаются экспериментально.

Ионизационное торможение. Впроцессе ионизационного торможения энергия заряженной частицы расходуется на ионизацию и возбуждение атомов среды, через которую она проходит.

Квантовомеханическое рассмотрение процесса торможения приводит к следующему выражению для потери энергии нере­лятивистской частицей на единице длины пути:

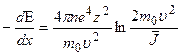, (1.2)

Здесь z и 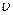— заряд и скорость частицы; п - число электронов в 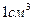; 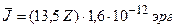- средний ионизационный потенциал атомов поглощающего вещества, где Z - заряд ядер среды; m 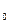- масса покоя электрона.

Таким образом, удельная потеря энергии заряженной частицей на ионизацию пропорциональна квадрату заряда частицы, концентрации электронов в среде, некоторой функции от скорости частицы и не зависит от массы частицы М.

Для частиц со скоростями, близкими к скорости света (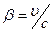 ~1), учет релятивистских эффектов приводит к добавочным слагаемым в формуле для удельных потерь:

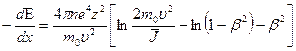. (1.3)

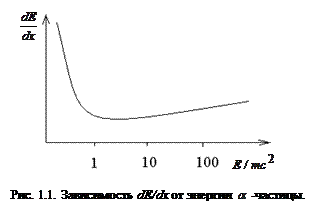
Это выражение известно как формула Бете. Графическая зависимость dE/dx от энергии -частицы представлена на рис. 1.1.

Пробег частицы R можно определить как расстояние, которое она проходит до момента полной потери энергии. Характерной особенностью -частиц является существование у них определенного пробега: треки -частиц одной энергии в камере Вильсона представляют собой прямые линии одной и той же длины с небольшим разбросом в ту или иную сторону (см. Приложение 1).

В энергетических -спектрах радиоактивных нуклидов часто наблюдается тонкая структура, т. е. -спектры зачастую состоят из дискретных линий, соответствующих -распаду на различные состояния дочерних ядер. Например, при распаде четно-чётных ядер, т. е. ядер, имеющих чётное число протонов и чётное число нейтронов, имеется интенсивная -линия, соответствующая -переходу между основными состояниями материнского и дочернего ядер, и одна или несколько линий с меньшей энергией и с меньшей интенсивностью, соответствующих -переходам на возбужденные состояния дочернего ядра. Эти линии соответствуют так называемым короткопробежным -частицам. Гораздо реже имеет место -распад возбужденных состояний атомных ядер (например, распад состояний ²¹⁴Ро). В этих случаях энергия -частиц больше энергии -группы из основного состояния, и такие -частицы называют длиннопробежными.

Величина пробега частицы определяется потерями энергии, которые происходят при ее движении. Потери эти различны для разных скоростей частиц.

1. При скоростях более 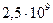см/с ( 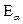> 15 МэВ) величина 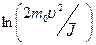в формуле (1.2) изменяется так медленно, что ее можно приближенно считать постоянной величиной порядка единицы. Раскроем выражение для -dE/dx:

.

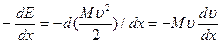Воспользовавшись формулой (1.2), получим 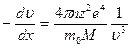. Тогда

.

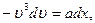
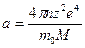Проинтегрируем это выражение: 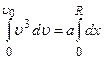. Здесь 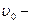начальная скорость частицы, R - величина ее пробега. Проинтегрируем последнее выражение и получим

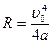. (1.4)

2. При скоростях -частиц (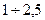)-10⁹ см/с (4 - 15 МэВ) можно приближенно считать, что ln(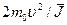) ~ B 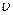. Тогда

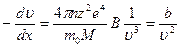
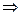
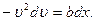
Интегрируя, получим

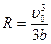. (1.5)

Для -частиц с энергиями 4-11 МэВ можно пользоваться соотношением

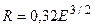. (1.6)

В этой формуле пробег -частиц в воздухе R (при 15 ºС и нормальном атмосферном давлении) выражается в сантиметрах, а энергия Е в мегаэлектронвольтах.

Если рассмотреть выражения для пробегов в данной среде разных частиц, имеющих одинаковые скорости, то можно убедиться, что они относятся как соответствующие частицам значения M/z². Например, пробеги -частиц и протонов, имеющих, равные скорости, относятся как

: .

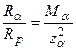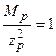При этом энергии -частиц и протонов отличаются в 4 раза.

На рис. 1.2 связь между пробегом и энергией частицы представлена в виде номограммы, при помощи которой по пробегу -частицы можно найти ее энергию, и наоборот.

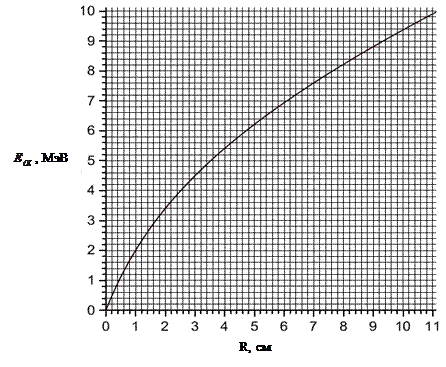
Рис. 1.2. Связь между энергией 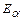и пробегом для 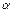- частиц в воздухе при атмосферном давлении 760 мм. рт. ст. и температуре 15 ºС.

Потеря энергии или торможение -частицы в веществе сопровождается ионизацией. Полной ионизацией называется число пар ионов, образованных -частицей на всем ее пути. Удельной ионизацией называют число пар ионов, образованных частицей на единице пути.

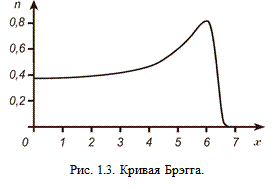
Удельная ионизация является не постоянной величиной, а функцией пройденного альфа-частицей расстояния. Если измерить зависимость удельной ионизации п от расстояния x, пройденного частицей, получится кривая, показанная на рис. 1.3. Эта зависимость называется кривой Брэгга.

Как видно из рисунка, с уменьшением скорости удельная ионизация возрастает, достигая острого максимума (пик Брэгга), и затем быстро падает до нуля.

Зная энергию -частицы и число пар ионов, образованных ею на протяжении всего пути, можно определить среднюю энергию, затрачиваемую -частицей на создание одной пары ионов. Оказалось, что эта величина почти не зависит от скорости частицы, но является важной характеристикой вещества. Табл. 1.1 дает ее значения для некоторых газов.

Таблица 1.1.
Газ	Е,эВ	Газ	Е,эВ
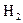	33,0		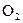33,3
Не	27,8	Ne	27,4
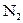	35,0	Ar	25,4

Разброс пробегов. Если мы возьмём достаточно тонкий источник - частиц, то все частицы выходят из него с одинаковой скоростью ( - частицы, испускаемые естественно-радиоактивными источниками, монохроматичны). Между тем, как можно убедиться на опыте, их пробег оказывается не одинаковым.

Если исследовать параллельный пучок - частиц, например, при помощи флуоресцирующего экрана, и подсчитать число сцинтилляций, увеличивая постепенно расстояние между источником и экраном, т.е. заставляя - частицы проходить все больший слой воздуха, то оказывается, что число частиц N в пучке остаётся приблизительно постоянным вплоть до определённого расстояния, а затем падает, но падает не сразу до нуля, а с некоторым наклоном (рис. 1.4, кривая 1). Если эту кривую продифференцировать и построить величину 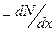в зависимости от толщины слоя, то получится кривая 2. Эта кривая имеет резкий максимум при 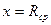, показывающий, что подавляющее большинство -частиц имеет определённый пробег с некоторым разбросом в ту или иную сторону. Величина 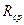называется средним пробегом. Разброс пробега называется страгглингом.

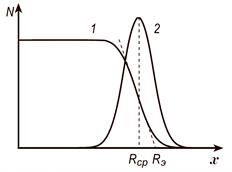
Рис. 1.4. Зависимость числа альфа-частиц, прошедших слой вещества, от толщины этого слоя.

Каковы же причины страгглинга?

Во-первых, дело во флуктуациях числа атомов на пути частицы. Число ионов, созданных частицей, т.е. потеря ею энергии, будет зависеть от этого числа. Если среднее число ионов, образуемых -частицей на длине её пробега N, то возможное отклонение от этого числа, согласно статистическому закону, равно 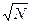. Среднее число пар ионов, образуемых частицей, движущейся со скоростью 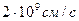, равно 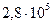. Флуктуация этого числа 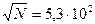, т.е. составляет 0,2 %. Однако, как показывает опыт, флуктуации в пробеге частиц составляют не 0,2 %, а значительно больше (около 2 %).

Второй причиной, вызывающей страгглинг, является перезарядка частиц при их движении через среду. Если направить пучок -частиц через камеру Вильсона с малой скоростью (пропустив их предварительно через фильтры перед камерой), то в треках -частиц можно видеть разрывы – это участки пути, на которых они являются нейтральными. При прохождении -частиц через вещество к ним может примкнуть один или два электрона. Таким образом, на всём пути частица имеет разный заряд. Опытами было установлено, что быстрая -частица движется, в основном, как двухзарядный ион или даже как нейтральная частица. Естественно, что перезарядка вызовет дополнительные флуктуации в ионизации, и значит, флуктуации в пробеге. Эта причина даёт 1,5 - 1,7 % разброса пробегов.

Помимо среднего пробега -частиц, существует понятие экстраполированного пробега. Кривые, подобные кривой 1 на рис. 1.4, почти прямолинейны на значительном расстоянии вблизи конца пробега, где имеется быстрый спад. Экстраполированный пробег получается путём продолжения этой почти прямой линии до пересечения её с осью абсцисс, и величина, соответствующая точке пересечения, принимается за величину пробега. Этот пробег всегда больше, чем средний. В таблицах приводят значения, как среднего, так и экстраполированного пробегов. В номограмме (рис. 1.2) даются значения среднего пробега.