Лекция №3
Тема: ВЕТРОВЫЕ ОТКЛОНЕНИЯ ПРОВОДОВ.
( лекция –1 час)
Ветровые отклонения одиночных проводов
При действии на провод равномерно распределенных по пролету вертикальной g и горизонтальной р нагрузок провод расположится в наклонной плоскости, как показано на рис. 3.1.
Обозначив через bх величину горизонтального статического отклонения провода в точке на расстоянии х от опоры и через у — провес провода в этой точке в направлении суммарной нагрузки q, из подобия треугольников получим
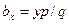
Наибольшее горизонтальное отклонение bmах провод получит в середине пролета, где имеет стрелу провеса f. Подставив в выражение х = l/2, получим
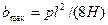
Выражения для определения ветровых отклонений одиночного провода можно использовать и при расчете ветровых отклонений контактного провода простых контактных подвесок, в которых контактный провод расположен в плане между точками подвеса по прямой линии. Вместо Н в выражение надо только подставить натяжение контактного провода К.
В случае, когда точки подвеса контактного провода у опор в плане смещены от оси пути в разные стороны (провод относительно оси пути расположен зигзагообразно), его отклонение от оси пути в горизонтальной плоскости при ветре будет определяться суммой отклонений b1 и b2 (рис. 3.2, а), значения которых могут быть найдены из выражений:
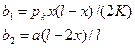
где, а – зигзаг провода
Отсюда получим статическое отклонение контактного провода bкх от оси пути в любой точке пролета, расположенной на расстоянии х от опоры:
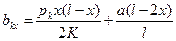
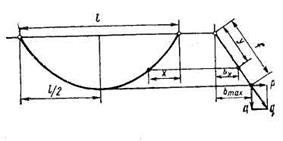
Рис. 3.1. Схема к определению статических отклонений одиночного провода ветром в различных точках пролета
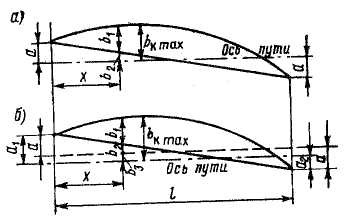
Рис. 3.2. Схемы к определению допустимой длины пролета на прямом участке пути
Исследование выражения показывает, что наибольшее отклонение контактного провода от оси пути (или, что то же, на прямом участке от оси токоприемника) будет в точке, расположенной от опоры на расстоянии
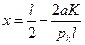
После подстановки этого значения х в выражение получим
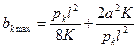
При различных зигзагах контактного провода у опор наибольшее его отклонение от оси пути при ветре можно определить следующим образом. Обозначим a — среднее значение зигзага контактного провода, т. е. примем
а = 0,5(а1+а2)
тогда согласно рис. 3.2, б получим
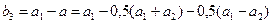
Наибольшее статическое отклонение провода в пролете согласно предыдущим выражениям
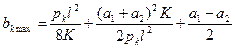
Наибольшее допустимое значение пролета будет в том случае, когда наибольшее отклонение провода bк max получится равным наибольшему допустимому отклонению провода от оси токоприемника bк доп- Поэтому, приняв в уравнении bк max = bк доп и решив его относительно l, получим выражение для определений допустимой длины пролета l mах на прямых участках пути при данных рк, K, bк доп и зигзагах а1 и а2:
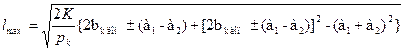
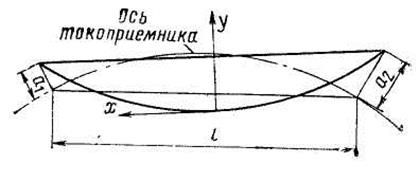
Рис. 3.3. Схема к определению допустимой длины пролета на кривом участке пути
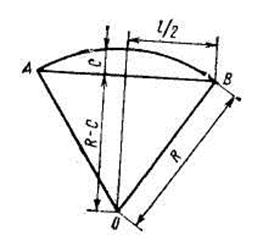
Рис. 3.4. Схема к определению стрелки кривой оси пути
При расчетах следует так выбирать знаки, чтобы получить меньшее значение l mах. Верхние знаки в формуле cooтветствуют направлению ветра со стороны зигзага а2, а нижние — со стороны а1.
Обычно на большей части прямых участков пути контактный провод монтируют с одинаковыми зигзагами, т. е. а1 = а2 (по абсолютной величине). Приняв в формуле а1=а2=а, получим выражение для определения допустимой длины пролета l на прямых участках пути при равных зигзагах провода
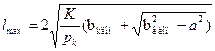
Рассматривая эту формулу, нетрудно заметить, что допустимая длина пролета растет с увеличением натяжения контактного провода К, допустимого отклонения bк доп и уменьшается с увеличением ветровой нагрузки рк и зигзага а.
Схема к определению допустимой длины пролета на кривом участке пути показана на рис. 3.3. Стрелку кривой оси пути С можно определить с помощью схемы, показанной на рис. 3.4. Для треугольника ОАВ имеем (l /2)2 + (R — С)2 = R2.
Раскрыв скобки и пренебрегая сравнительно малым значением С2, получим
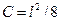
Нетрудно показать, что максимальное ветровое отклонение контактного провода от оси токоприемника на кривом участке пути радиуса R при неодинаковых зигзагах контактного провода у опор можно найти по формуле
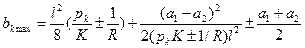
При неодинаковых зигзагах а1 и а2 максимальное ветровое отклонение контактного провода будет несколько смещено от середины пролета. Это смещение определяется выражением
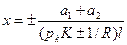
Если в уравнении принять bк max = bк доп и решить его относительно l, получим выражение для определения допустимой длины пролета l mах на кривых участках пути радиуса R при данных рк, К, bк доп и зигзагах а1 и а2:
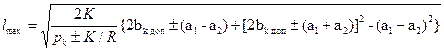
При одинаковых зигзагах а1=а2=а максимальное статическое отклонение контактный провод получит в середине пролета:
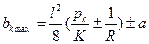
и соответственно
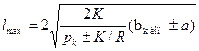
Все приведенные выше выражения для bк max и l mах были выведены без учета изменения упругого прогиба опор на уровне контактного провода γk под действием ветровой нагрузки на опоры и провода. Значение γk может достигать ±65 мм. Поэтому при определении длин пролетов контактных подвесок значение ук необходимо обязательно учитывать. В этом случае формулы для определения bк max и l mах примут вид:
для прямых участков и кривых участков пути при одинаковых зигзагах контактного провода у опор
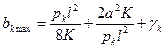
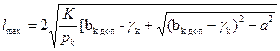
 2015-06-05
2015-06-05 3013
3013






