Індивідуальне завдання «Гладкі многовиди» (40 балів)
Задача1.(20 б.)
Довести, що 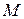 – гладкий многовид,
– гладкий многовид, 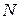 - топологічний простір. Побудувати гомеоморфізм
- топологічний простір. Побудувати гомеоморфізм 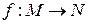
1. 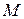 – площина
– площина 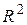 ,
, 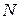 – напівсфера радіусу 5.
– напівсфера радіусу 5.
2. 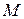 – площина
– площина 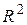 ,
, 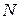 – еліптичний параболоїд.
– еліптичний параболоїд.
3. 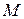 – площина
– площина 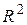 ,
, 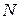 – параболічний циліндр.
– параболічний циліндр.
4. 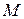 – коло радіусу 3,
– коло радіусу 3, 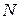 – опуклий шестикутник.
– опуклий шестикутник.
5. 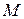 – одиничне коло,
– одиничне коло, 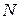 –еліпс.
–еліпс.
6. 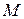 – сфера,
– сфера, 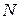 – поверхня куба.
– поверхня куба.
7. 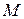 –відкритий круг,
–відкритий круг, 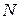 – одна порожнина двопорожнинного гіперболоїду.
– одна порожнина двопорожнинного гіперболоїду.
Задача 2. (20 б.)
1. На множині 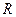 побудовано дві карти:
побудовано дві карти: 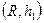 і
і 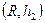 , де
, де 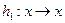 ,
, 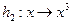 . Знайти клас гладкості функцій, які задають відображення переходу.
. Знайти клас гладкості функцій, які задають відображення переходу.
2. Побудувати атлас з двох карт на множині 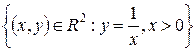
3. Довести, що множина точок  є елементарним гладким многовидом.
є елементарним гладким многовидом.
4. На множині 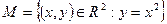 розглядаються підмножини
розглядаються підмножини 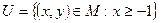 і
і 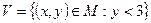 . Задано також відображення
. Задано також відображення 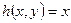 ,
, 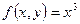 ,
, 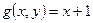 . Які з пар
. Які з пар 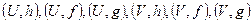 є картами на
є картами на 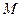 ?
?
5. На множині 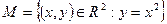 розглядаються підмножини
розглядаються підмножини 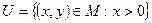 і
і 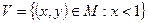 . Задано також відображення
. Задано також відображення 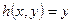 ,
, 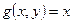 . Довести, що пари
. Довести, що пари 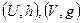 є картами на заданій множині. Взяти деяку точку з множини
є картами на заданій множині. Взяти деяку точку з множини 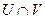 і знайти її локальні координати в кожній з карт.
і знайти її локальні координати в кожній з карт.
6. Дан набор  координат тензора типа
координат тензора типа 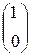 в системе координат
в системе координат 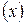 в точке (0,0). Найти его координаты в системе
в точке (0,0). Найти его координаты в системе 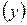 в этой же точке, если эти системы координат связаны уравнениями
в этой же точке, если эти системы координат связаны уравнениями 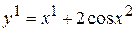 ,
, 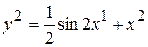 .
.
7. Найти координаты метрического тензора 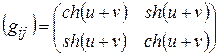 в новой криволинейной системе координат
в новой криволинейной системе координат 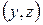 в точке
в точке 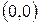 , если
, если 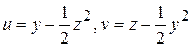 .
.
 2015-06-26
2015-06-26 188
188






