Общее уравнение прямой
Прямую в пространстве можно рассмотреть, как линию пересечения двух плоскостей:
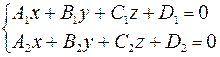 (1) – это общее уравнение прямой
(1) – это общее уравнение прямой
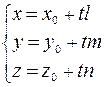 (2) – параметрические уравнения прямой в пространстве
(2) – параметрические уравнения прямой в пространстве
l, m, n – направляющие коэффициент прямой.
Канонические уравнения прямой.
Выразим t: 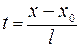 ;
;  ;
; 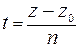 или
или
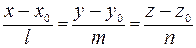 (3)
(3)
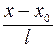 =
= 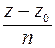 – плоскость параллельная оси OY и
– плоскость параллельная оси OY и
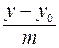 =
= 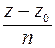 – плоскость параллельная оси OX, то есть плоскости, проектирующие прямую на координатные плоскости OXZ и OYZ.
– плоскость параллельная оси OX, то есть плоскости, проектирующие прямую на координатные плоскости OXZ и OYZ.
Это уравнения двух плоскостей, их пересечение – прямая линия.
Числа l, m, n называются направляющими коэффициентов прямой.
Условие параллельности прямых:
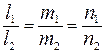
Условие перпендикулярности:
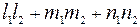 = 0
= 0
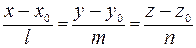
Ax + By + Cz + D = 0
N = (A,B,C)
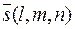
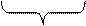
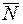 ·
· 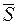 =
= 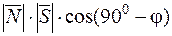
sinφ
sinφ = 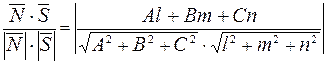
Al + Bm + Cn = 0 – прямая 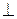
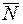
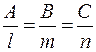 – прямая ||
– прямая || 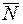
Уравнение первой степени относительно прямой
A 1 x 1 + A 2 x 2 = B – прямая на плоскости
Уравнение первой степени относительно прямой
A 1 x 1 + A 2 x 2 + A 3 x 3 = B – плоскость в трехмерном пространстве.
Уравнение первой степени относительно прямой
A 1 x 1 + A 2 x 2 +... + Anxn = B – гиперплоскость в n -мерном пространстве.
Если имеем точку M 1(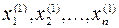 ) в n -мерном пространстве и гиперплоскость A 1 x 1 + A 2 x 2 +... + Anxn – B = 0, то расстояние от точки до гиперплоскости:
) в n -мерном пространстве и гиперплоскость A 1 x 1 + A 2 x 2 +... + Anxn – B = 0, то расстояние от точки до гиперплоскости:
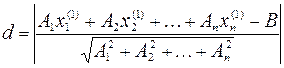
Вектором называется направленный отрезок, для которого указано его начало и конец:
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Произведением ненулевого вектора 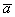 на число
на число 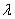 является такой вектор
является такой вектор  , длина которого равна
, длина которого равна 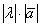 , причём векторы
, причём векторы 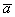 и
и  сонаправлены при
сонаправлены при 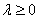 и противоположно направлены при
и противоположно направлены при 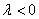 .
.
Правило умножения вектора на число легче понять с помощью рисунка:
1) Правило сложения векторов. Рассмотрим два вектора плоскости 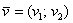 и
и 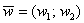 . Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:
. Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:
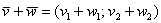 .
.
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы 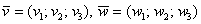 , то их суммой является вектор
, то их суммой является вектор 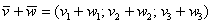 .
.
 2015-06-28
2015-06-28 288
288






