2015-06-28
316Решить методом Гаусса СЛАУ.
1) 2,74x1-1,18x2+3,17x3 = 2,18 2) 4x1+3x2+2x3+x4 = 3
1,12x1+0,83x2-2,16x3 = -1,15 3x1+6x2+4x3+2x4 = 6
0,81x1+1,27x2+0,76x3 = 3,23 2x1+4x2+6x3+3x4 = 4
3) 7,9x1+5,6x2+5,7x3-7,2x4 = 6,68 4) 6x1-x2-x3 = 11,33
8,5x1-4,8x2+0,8x3+3,5x4 = 9,95 -x1+6x2-x3 = 32
4,3x1+4,2x2-3,2x3+9,3x4 = 8,6 -x1-x2+6x3 = 42
3,2x1-1,4x2-8,9x3+3,3x4 = 1
Решить СЛАУ методом Гаусса с выбором главного элемента по столбцу.
5) 2x1+4x2-7x3 = 1 6) –x1+3x2+x3 = 4
3x1+6x2+x3 = 0 2x1-6x2-x3 = 3
x1+3x2+2x3 = -1 2x1+5x2+3x3 = 1
7) 3x1-x2+3x3 = 0
6x1-2x2+x3 = 1
x1+x2-x3 = -2
Решить СЛАУ методом Гаусса с выбором главного элемента по строке.
8) x1+2x2-7x3+4x4 = 1 9) 2x1+x2+2x3-x4 = -3
5x1+10x2+x3-3x4 = 2 4x1+2x2-x3+2x4 = 3
x1+5x2-x3+x4 = -2 x1-x2+x3-x4 = 1
2x1+x2+3x3-x4 = -1 x1+3x2-2x3+x4 = 0
10) 3x1-x2+x3-5x4 = 0
9x1-3x2+6x3-5x4 = 2
2x1+x2-4x3+2x4 = -1
x1-3x2+2x3-x4 = 3
Вычислить определитель матрицы, пользуясь схемой Гаусса.
11) D=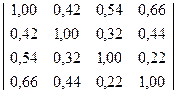 
12) D=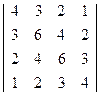 
13) D=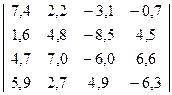 
14) D=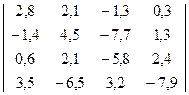 
Вычислить обратную матрицу по схеме Гаусса.
15) A=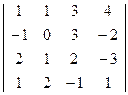 
16) A=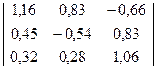 
17) A=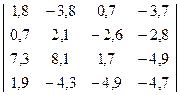 
Решить СЛАУ методом квадратного корня.
18) 1,65x1-1,76x2+0,77x3 = 2,15 19) 0,53x1-0,75x2+1,83x3 = 0,68
-1,76x1+1,04x2-2,61x3 = 0,82 -0,75x1+0,68x2-1,19x3 = 0,95
0,77x1-2,61x2-3,18x3 = -0,73 -0,75x1+0,68x2-1,19x3 = 0,95
20) 2,56x1+0,67x2-1,78x3 = 1,14 21) 4,25x1-1,48x2+0,73x3 = 1,44
0,67x1-2,67x2+1,35x3 = 0,66 -1,48x1+1,73x2-1,85x3 = 2,73
-1,78x1+1,35x2-0,55x3 = 1,72 0,73x1-1,85x2+1,36x3 = -0,64
|
|
|
Решить СЛАУ методом правой прогонки.
22) -3x1+2x2 = 1, x1+3x2-2x3 = 4, 2x2+6x3+3x4 = 0, -7x3+9x4+x5 = -3,
8x4+x5 = -7
23) 2x1+x2 = 1, x1+3x2+x3 = 2, x2+4x3+2x4 = -1, 2x3+5x4+2x5 = 0, 2x4+x5 = 3
24) x1+5x2 = 0, x1+7x2-4x3 = 1, -x2+3x3-2x4 = 4, 2x3+8x4-x5 = 3, x4-5x5 = 0
25)–x1+3x2 = 7, 2x1+9x2-x3 = 4, 3x2+5x3+x4 = -2, x3-6x4-x5 = 1, 2x4+4x5 = 1
Ответы:
1) x1=0,0970, x2=1,7728, x3=1,2638
2) x1=0, x2=1, x3=-1, x4=2
3) x1=0,9671, x2=0,1248, x3=0,4263, x4=0,5679
4) x1=4,6661, x2=7,6189, x3=9,0475
5) x1=1,6087, x2=-0,7826, x3=-0,1304
6) x1=-5,5454, x2=-4,1818, x3=11,0000
7) x1=-0,5, x2=-2,1, x3=-0,2
8) x1=0,5258, x2=-0,4124, x3=-1,0515, x4=-1,5155
9) x1=1,1538, x2=-1,6154, x3=-1,9231, x4=-0,1538
10) 10) x1=-0,0584, x2=-1,0467, x3=0,0514, x4=0,1846
11) D=0,2861
12) D=125
13) D=-1618,29
14) D=541,78
15) A-1=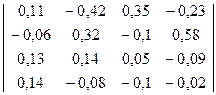 
16) A-1=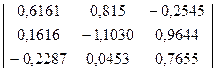 
17) A-1=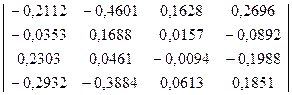 
18) x1=79,0915, x2=59,8977, x3=-29,7806
19) x1=4,8666, x2=17,4986, x3=6,1337
20) x1=-1,8263, x2=-2,9115, x3=-4,3630
21) x1=0,1520, x2=-2,4581, x3=-3,8960
22) x1=0,2686, x2=0,9029, x3=-0,5113, x4=0,4207, x5=-10,3657
23) x1=-5, x2=11, x3=-26, x4=46, x5=-89
24) x1=-37,3305, x2=7,4661, x3=3,4831, x4=-0,5085, x5=-0,1017
25) x1=-3,5997, x2=1,1334, x3=-0,9983, x4=-0,4088, x5=0,4544
