Прямая с угловым коэффициентом

Рассмотрим любую прямую, не параллельную оси Ox. Введем понятие угла наклона прямой к оси Ox. Предположим, что рассматриваемая прямая пересекает ось Ox в точке А (рис. 2).

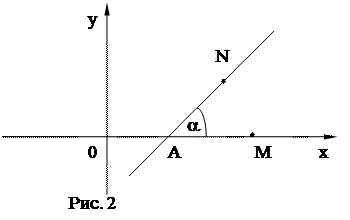Возьмем на оси Ox произвольную точку M, лежащую по ту сторону от точки A, куда направлена ось Ox, а на рассматриваемой прямой произвольную точку N, лежащую по ту сторону от точки A, куда направлена ось Oy. Угол 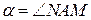назовем углом наклона данной прямой к оси Ox.

Если прямая параллельна оси Ox или совпадает с ней, то угол наклона этой прямой к оси Ox мы будем считать равным нулю.

Тангенс угла наклона прямой к оси Ox назовем угловым коэффициентом этой прямой. Если обозначить буквой k угловой коэффициент данной прямой, а буквой 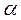угол наклона этой прямой к оси Ox, то по определению можно записать .

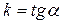Заметим, что для прямой, параллельной оси Ox, угловой коэффициент равен нулю, а для прямой, перпендикулярной оси Ox, угловой коэффициент не существует (в последнем случае иногда формально говорят, что угловой коэффициент “обращается в бесконечность”).

Для того чтобы вывести уравнение прямой, проходящей через заданную точку M₁(x₁,y₁) и имеющей данный угловой коэффициент k, умножим обе части канонического уравнения (7) на m и учтем, что 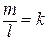. Мы получим искомое уравнение в виде

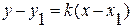(10)

Если мы теперь обозначим через b постоянную 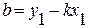, то уравнение (10) примет вид

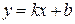(11)

Уравнение (11) называется уравнением прямой с угловым коэффициентом. В этом уравнении k обозначает угловой коэффициент данной прямой, а b представляет собой величину отрезка, отсекаемого данной прямой на оси Oy, начиная от начала координат.

3. Взаимное расположение двух прямых.

а) Пусть сначала две прямые L₁ и L₂ заданы общими уравнениями

Aa₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0.

Так как нормальным вектором прямой L₁ является вектор n₁ = {A₁,B₁}, а нормальным вектором прямой L₂ является вектор n₂ = {A₂, B₂}, то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла 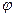между векторами n₁ и n₂.

Из определения скалярного произведения n₁n₂ = 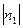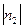cos 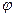и из выражения в координатах для длин векторов n₁ и n₂ и их скалярного произведения получим

cos 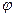= 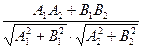(21)

Итак, угол 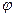между прямыми L₁ и L₂ определяется с помощью формулы (21).

Условие параллельности прямых L₁ и L₂, эквивалентно условию коллинеарности векторов n₁ и n₂, заключается в пропорциональности координат этих векторов, т.е. имеет вид

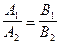(22)

Условие перпендикулярности прямых L₁ и L₂ может быть извлечено из формулы (21) (при cos 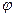= 0) или выражено равенством нулю скалярного произведения 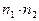. Оно имеет вид

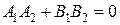(23)

б) Пусть теперь две прямые L₁ и L₂ заданы каноническими уравнениям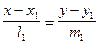и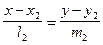

Так как направляющими векторами прямых L₁ и L₂ служат векторы q₁ = { l₁, m₁ } и q₂ = { l₂, m₂ }, то в полной аналогии со случаем а) мы получим:

1) формулу для угла 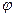между прямыми L₁ и L₂:

cos 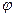= 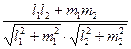, (21¢)

2) условие параллельности прямых L₁ и L₂:

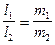, (22¢)

3) условие перпендикулярности прямых L₁ и L₂:

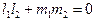. (23¢)

в) Пусть, наконец, две прямые L₁ и L₂ заданы уравнениями с угловым коэффициентом

y = k₁x + b₁ и y = k₂x + b₂

Мы получаем следующую формулу для определения угла :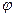

tg 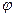= 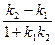. (21¢¢)

Прямые параллельны, когда тангенс угла между ними равен нулю, т.е. условие параллельности имеет вид

k₁ = k₂ (22¢¢)

(при этом числитель в (21¢¢) равен нулю, а знаменатель строго положителен).

Условие перпендикулярности прямых L₁ и L₂ также можно получить из (21¢¢). Оно отвечает случаю, когда тангенс угла 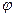не существует, т.е. случаю обращения знаменателя формулы (21¢¢) в нуль: k₁k₂+ 1 = 0.

Итак, условие перпендикулярности прямых L₁ и L₂ имеет вид

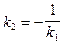. (23¢¢)