на плоскости и в пространстве

Тема: Аналитическая геометрия

Лекция № 7 “Прямая на плоскости. Основные задачи”

1. Общее уравнение прямой.

Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами и по этой плоскости порождает линию.

О1. Любое соотношение 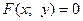(имеющее смысл в области вещественных чисел), где 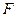некоторое выражение, связывающее переменные величины и , называется уравнением с двумя неизвестными, которое определяет линию. Точки, принадлежащие линии, удовлетворяют приведенному соотношению, а точки вне линии – не удовлетворяют.

О2. Порядок линии определяется по высшему показателю степени переменных и или по сумме показателей степени в произведении этих величин.

Пример 1. а) 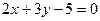– линия первого порядка; точка 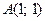удовлетворяет этому соотношению, а точка, например, 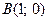– ему не удовлетворяет;

б) 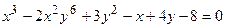– линия восьмого порядка;

в) 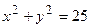и 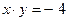– линии второго порядка.

Рассмотрим другое определение линии:

О2. Геометрическое место точек, координаты которых удовлетворяют уравнению 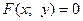, называется линией, а само уравнение 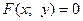– уравнением линии.

О3. Общим уравнением прямой называется уравнение первого порядка вида .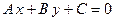

Рассмотрим частные случаи этого уравнения:

а) 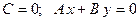– прямая проходит начало системы координат ( Рис. 20 )

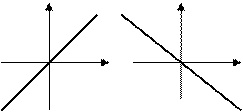
Рис. 20. Прямая, проходящая

через начало координат.

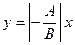
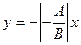
б) 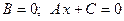– прямая проходит параллельно оси ординат ( Рис. 21 )

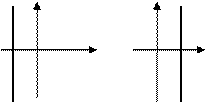
Рис. 21. Прямая, проходящая параллельно

оси ординат .

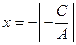
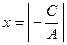
в) 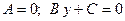– прямая проходит параллельно оси абсцисс ( Рис. 22 )

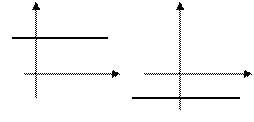
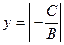Рис. 22. Прямая, проходящая

параллельно оси абсцисс .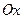

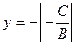
2. Виды уравнений прямой.

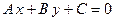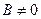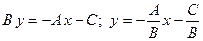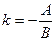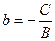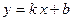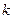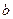1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой , в котором коэффициент . Разрешим общее уравнение прямой относительно переменной : . Обозначим через и , тогда уравнение примет вид , которое называется уравнением прямой с угловым коэффициентом. Выясним геометрический смысл параметров и . При 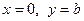, т.е. параметр 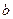показывает, какой величины отрезок отсекает прямая на оси ординат, считая от начала отсчета. При 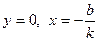, т.е. прямая отсекает на оси абсцисс отрезок 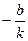( Рис. 23 ).

,

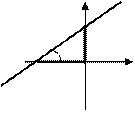
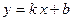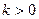
Рис. 23. Отрезки, отсекаемые прямой на

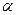
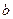координатных осях.

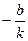
Из рисунка видно, что 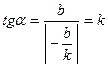, т.е. угловой коэффициент 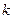определяет тангенс угла наклона прямой к положительному направлению оси абсцисс .

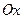2. Уравнение прямой в отрезках. Пусть в общем уравнении прямой параметр 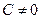. Выполним следующие преобразования

; .

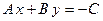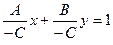Обозначим через 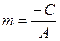и 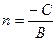, тогда последнее равенство перепишется в виде 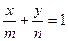, которое называется уравнением прямой в отрезках. Выясним геометрический смысл величин 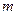и 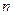( Рис. 24 ). При 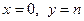, т.е. параметр 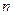показывает, какой величины отрезок отсекает прямая на оси ординат, считая от начала отсчета. При 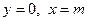, т.е. прямая отсекает на оси абсцисс отрезок 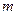. Это означает, что прямая проходит через две точк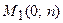и и .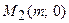

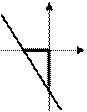
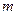Рис. 24. Отрезки, отсекаемые прямой на

координатных осях.

, ,

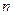
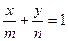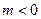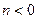
Пример 2. Построить прямую 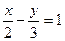(самостоятельно).

3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой 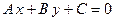, которая проходит через две известные точк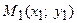и и 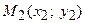. Так как точк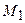и и 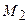лежат на прямой, то их координаты удовлетворяют общему уравнению прямой, т.е. выполняются равенства 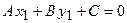и 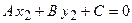. Вычтем первое из этих равенств из общего уравнения прямой и из второго равенства:

,

.

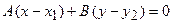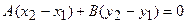Пусть 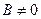, тогда полученные равенства можно преобразовать к виду

, .

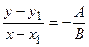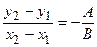Отсюда находим, что 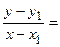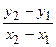или 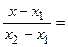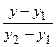. Полученное уравнение называется уравнением прямой, проходящей через две заданные точк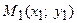и и .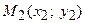

Пример 3. Составить уравнение прямой, проходящей через точк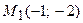и и 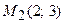(самостоятельно).

4. Уравнение прямой, проходящей через заданную точку 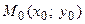параллельно заданному вектору 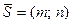( каноническое уравнение прямой ). Пусть прямая проходит через заданную точку 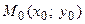параллельно вектору .

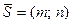О4. Вектор 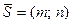называется направляющим вектором прямой.

Возьмем на прямой произвольную точку 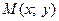и создадим вектор 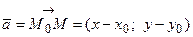( Рис. 25 ).

Рис. 25. Прямая, проходящая через

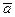данную точку параллельно направ-

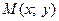ляющему вектору.

В силу того, что вектора 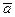и 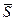коллинеарны, то воспользуемся первым условием коллинеарности: отношения соответствующих проекций равны между собой .

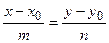О5. Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо кано-ническим уравнением прямой.

5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру , то получим параметрическое уравнение прямой .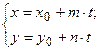

3. Основные задачи.

1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 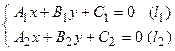. Требуется найти координаты точки пересечения этих прямых. Для того чтобы вычислить координаты точки пересечения , необходимо решить вышеприведенную систему линейных алгебраических уравнений, так как координаты точки должны одновременно удовлетворять уравнениям прямых 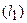и .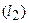

2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами

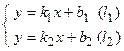. Требуется найти угол между этими прямыми ( Рис. 26 ).

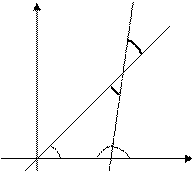
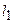
Рис. 26. Угол между двумя прямыми.

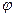
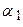
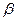
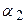
Из рисунка видно, что 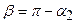, а угол 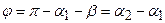. Вычислим :

.

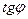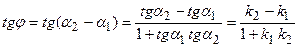Наименьший угол между пересекающимися прямыми определим формулой

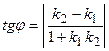. Из полученной формулы видно:

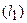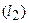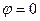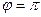а) если прямые и параллельны или совпадают ( или ), то 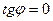. Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой .

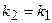а) если прямые 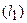и 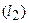перпендикулярны (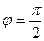), то 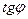не существует. Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением .

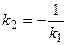Пример 4. Определить угол между прямыми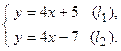

В силу того, что 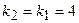, то прямые параллельны, следовательно, .

Пример 5. Выяснить взаимное расположение прямых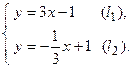

Так как угловые коэффициенты 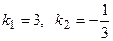и связаны между собой соотношением 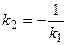, то прямые взаимно перпендикулярны.

3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки 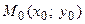на прямую 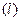. Если прямая 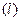задана общим уравнением, то расстояние от точки до прямой

определяется формулой: 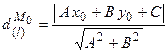. Если прямая 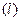задана уравнением прямой с угловым коэффициентом, то расстояние от точки до прямой определяется формулой: .

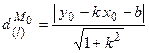Лекция № 8 “Кривые второго порядка”

1. Окружность.

О1. Кривой второго порядка называется линия, описываемая уравнением .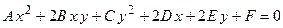

З1. Если коэффициенты 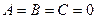, уравнение кривой II порядка вырождается в уравнение прямой.

При определенных значениях параметров, входящих в это уравнение, оно дает канонические уравнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.

О2. Окружностью называется геометрическое место точек равноудаленных от выделенной точки 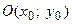, называемой центром окружности, на

расстояние , которое называется радиусом окружности.

Получим уравнение окружности ( Рис. 27 ). Пусть точка 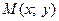лежит на окружности

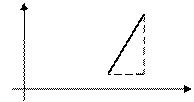
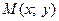
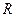Рис. 27. Вывод уравнения окружности.

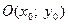
Из рисунка видно, что по теореме Пифагора 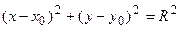, которое определяет уравнение окружности ( Рис. 28 ).

Рис. 28. Окружность.

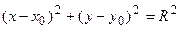
Если 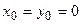, то уравнение принимает вид 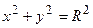, которое называется каноническим уравнением окружности.

2. Эллипс.

О3. Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек 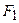и 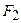, называемых фокусами эллипса, есть величина постоянная и равная .

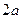Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы 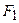и 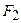были расположены на оси абсцисс симметрично относительно начала отсчета ( Рис. 29 ). Пусть точка 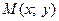лежит на эллипсе, фокусы которого имеют координаты 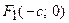и .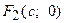

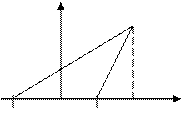
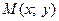
Рис. 29. Вывод уравнения эллипса.

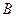
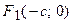
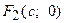
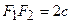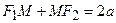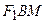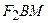Расстояние между фокусами (фокусное расстояние) равно . Согласно определению эллипса имеем . Из треугольников и по теореме Пифагора найдем

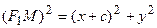и ,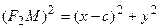

соответственно. Следовательно, согласно определению имеем

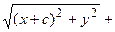
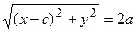или .

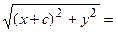
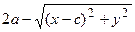Возведем обе части равенства в квадрат, получим

.

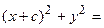
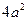
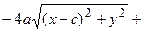
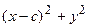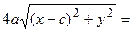
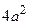
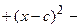
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 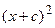. Раскроем разность квадратов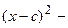 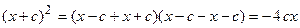. Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно

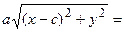
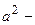
перейдет в уравнение 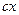. Вновь возведем обе части равенства в квадрат 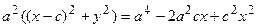. Раскрывая все скобки в правой части уравнения, получим 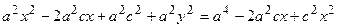. Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим 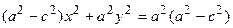. Введем обозначение для разности, стоящей в скобках 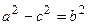. Уравнение принимает вид 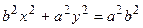. Разделив все члены уравнения на величину 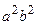, получаем каноническое уравнение эллипса: 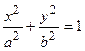. Если 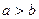, то эллипс вытянут вдоль оси 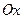, при выполнении противоположного неравенства – вдоль оси 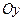(при этом фокусы тоже расположены на этой оси). Проанализируем полученное уравнение. 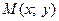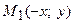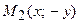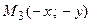Если точка принадлежит эллипсу, то ему принадлежат и точки , и , следовательно, эллипс симметричен относительно координатных осей, которые в данном случае будут называться осями симметрии эллипса. Найдем координаты точек пересечения эллипса с координатными осями:

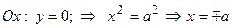, т.е. точками пересечения эллипса с осью абсцисс будут точк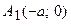и и ;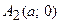

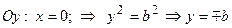, т.е. точками пересечения эллипса с осью ординат будут точк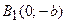и и 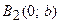( Рис. 30 ).

О4. Найденные точки называются вершинами эллипса.

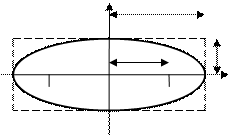
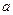
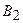
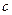
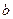Рис. 30. Вершины, фокусы и параметры

эллипса.

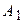
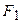
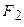
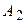
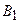
О5. Если 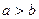, то параметр 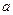называется большой, а параметр 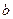– малой полуосями эллипса.

О6. Эксцентриситетом эллипса называется отношение фокусного расстояния к большой полуоси эллипса .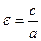

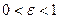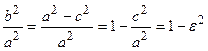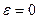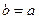Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству . Кроме того, эта характеристика описывает форму эллипса. Для демонстрации этого факта рассмотрим квадрат отношения малой полуоси эллипса к большой полуоси . Если , то и эллипс вырождается в окружность. Если 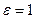, то и эллипс вырождается в отрезок .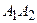

Пример 1. Составить уравнение эллипса, если его большая полуось 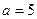, а его эксцентриситет .

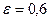Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 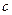: 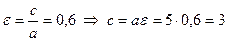. Зная параметр 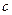, можно вычислить малую полуось эллипса 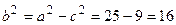. Следовательно, каноническое уравнение заданного эллипса имеет вид: .

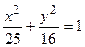3. Гипербола.

О7. Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек 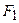и 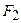, называемых фокусами гиперболы, есть величина постоянная и равная .

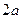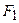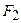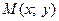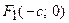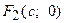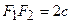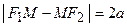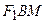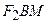Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы и были расположены на оси абсцисс сим-метрично относительно начала отсчета. Пусть точка лежит на гиперболе, фокусы которой имеют координаты и ( Рис. 31 ). Расстояние между фокусами (фокусное расстояние) равно . Согласно О7. для гиперболы имеем . Из треугольников и по теореме Пифагора найдем 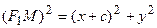и 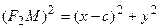, соответственно. Следовательно, согласно определению имеем

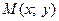
Рис. 31. Вывод уравнения гиперболы.

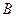
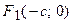
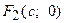
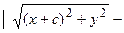
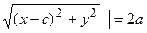или .

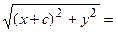
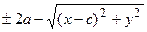Возведем обе части равенства в квадрат, получим

.

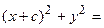
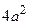
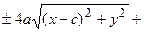
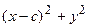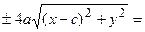
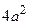
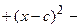
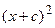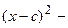
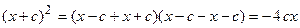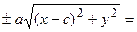
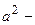
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим . Раскроем разность квадратов . Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение 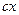. Вновь возведем обе части равенства в квадрат 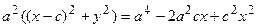. Раскрывая все скобки в правой части уравнения, получим 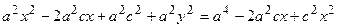. Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим 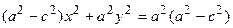. Введем обозначение для разности, стоящей в скобках 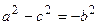. Получим

.

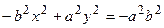Разделив все члены уравнения на величину 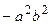, получаем каноническое уравнение гиперболы: 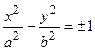. Для знака “+” фокусы гиперболы расположены на оси 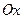, вдоль которой вытянута гтпербола. Для знака “–” фокусы гиперболы расположены на оси 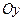, вдоль которой вытянута гтпербола. Проанализируем полученное уравнение. Если точка 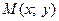принадлежит гиперболе, то ей принадлежат и симметриичные точк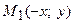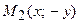и , и 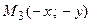, следовательно, гипербола симметрична относительно координат-ных осей, которые в данном случае будут называться осями симметрии гиперболы ( Рис. 32 ). Найдем координаты точек пересечения гиперболы с координатными осями:

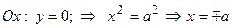, т.е. точками пересечения гиперболы с осью абсцисс будут точк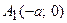и и ;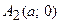

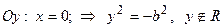, т.е. гипербола не пересекает ось ординат.

О8. Найденные точк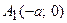и и 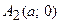называются вершинами ги-перболы.

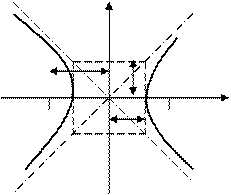
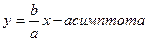
Рис. 32. Асимптоты и параметры гипер-

гиперболы.

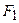
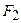
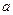
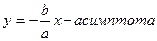
Докажем, что при возрастании (убывании) переменной гипербола неограниченно приближается к прямым 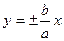, не пересекая эти прямые. Из уравнения гиперболы находим, что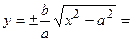 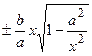. При неограниченном росте (убывании) переменной величина 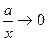, следовательно, гипербола будет неограниченно приближаться к прямым .

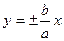О9. Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.

В данном конкретном случае параметр 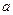называется действительной, а параметр 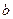– мнимой полуосями гиперболы.

О10. Эксцентриситетом гиперболы называется отношение фокусного

расстояния к действительной полуоси гиперболы .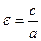

Из определения эксцентриситета гиперболы следует, что он удовлетворяет

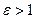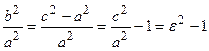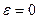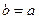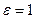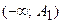неравенству . Кроме того, эта характеристика описывает форму гиперболы. Для демонстрации этого факта рассмотрим квадрат отношения мнимой полуоси гиперболы к действительной полуоси . Если эксцентриситет , то и гипербола становится равнобочной. Если , то и гипербола вырождается в два полубесконечных отрезка и .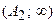

Пример 2. Составить каноническое уравнение гиперболы, если мнимая полуось 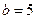и гипербола проходит через точку .

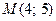Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины: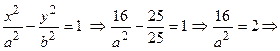

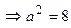. Следовательно, каноническое уравнение гиперболы имеет вид .

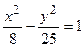4. Парабола.

О11. Параболой называется геометрическое место точек равноудаленных от выделенной точки 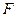, называемой фокусом параболы, и прямой 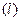, называемой директрисой.

Выведем каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус 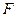лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс ( Рис. 33 ). Пусть точка 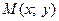принадлежит параболе:

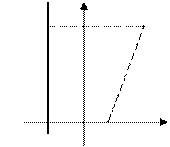
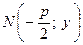
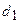
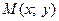
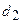Рис. 33. Вывод уравнения параболы.

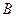
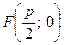
Вычислим расстояния от точки 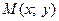до фокуса и директрисы

; .

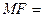
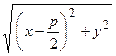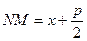По определению параболы эти расстояния равны, следовательно,

.

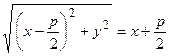Возведем обе части уравнения в квадрат

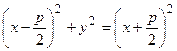или .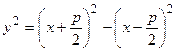

Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: 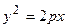(а также аналогичные ему, см. Рис. 34). Найдем координаты точек пересечения параболы с координатными осями:

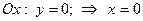, т.е. 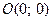– точка пересечения параболы с осью абсцисс;

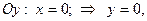, т.е. 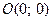– точка пересечения параболы с осью ординат.

О12. Точка 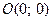называется вершиной параболы.

Если точка 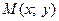принадлежит параболе, то ей принадлежат и точка 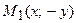, следовательно, парабола симметрична относительно оси абсцисс.

Пример 3. Дано уравнение параболы 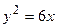. Определить координаты фокуса параболы и составить уравнение параболы.

Так как из уравнения параболы 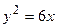следует, что 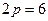, следовательно 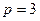. Таким образом, фокус этой параболы лежит в точке 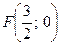, а уравнение параболы имеет вид .

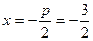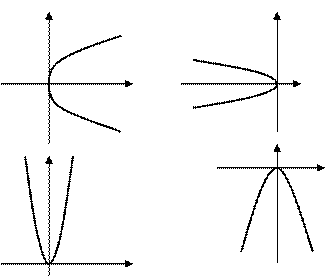
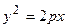
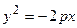
Рис. 34. Параболы и их

уравнения.

Лекция № 10 “Плоскость в пространстве”

1. Общее уравнение плоскости.

О1. Уравнение вида 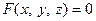отображает поверхность в пространстве.

О2. Порядок поверхности определяется по высшему показателю степени переменных , и 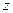или по сумме показателей степени в произведении этих величин.

О3. Уравнение вида 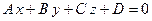называется общим уравнением плоскости.

Рассмотрим частные случаи приведенного уравнения:

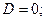
1) 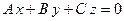. Из этого уравнения видно, что точка 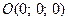удовлетворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат ( Рис. 44 ).

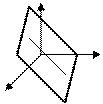
Рис. 44. Плоскость, проходящая через начало координат.

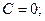
2) 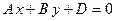. Этому уравнению удовлетворяет любое значение переменной 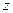, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (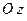) ( Рис. 45 ).

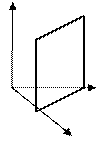
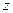
Рис. 45. Плоскость, проходящая параллельно оси

аппликат.

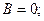
– плоскость параллельна оси ординат ();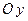

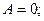
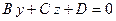– плоскость параллельна оси абсцисс ().

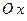З1. При отсутствиив уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.

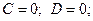
3) 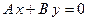– плоскость проходит через начало отсчета параллельно оси аппликат ( Рис. 46 ).

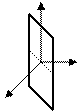
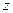
Рис. 46. Плоскость, проходящая через начало координат

параллельно оси аппликат.

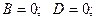
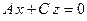– плоскость проходит через начало координат параллельно оси ординат;

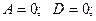
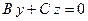– плоскость проходит через начало координат параллельно оси абсцисс.

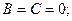
4) 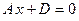– плоскость проходит через точку 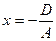параллельно плоскости 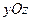( Рис. 47 ).

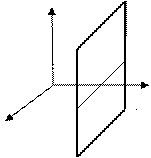
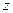
Рис. 47. Плоскость, проходящая параллельно

координатной плоскости .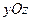

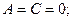
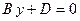– плоскость проходит через точку 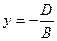параллельно плоскости ;

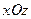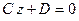– плоскость проходит через точку 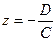параллельно плоскости .

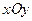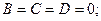
5) – уравнение описывает плоскость 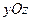( Рис. 48 ).

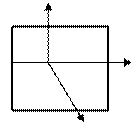
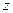
Рис. 48. Координатная плоскость .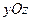

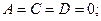
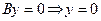– уравнение описывает плоскость ;

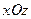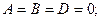
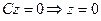– уравнение описывает плоскость .

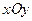2. Другие уравнения плоскости.

а) Уравнение плоскости в отрезках. Пусть в уравнении 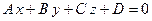коэффициент 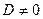, тогда выполним следующие преобразования

.

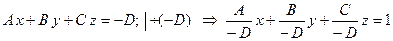Введем следующие обозначения 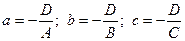, тогда уравнение примет вид 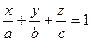, которое называется уравнением плоскости в отрезках. Найдем точки пересечения плоскости с координатными осями:

.

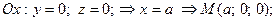
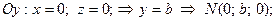
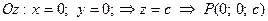Откладывая на координатных осях точк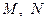и и 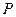, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры 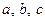положительные) ( Рис. 49 ):

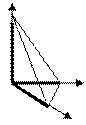
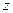
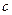Рис. 49. Отрезки, отсекаемые плоскостью на

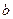координатных осях.

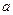
Из рисунка видно, что числа 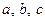показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.

б) Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 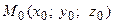, через которую проходит плоскость перпендикулярно к заданному вектору

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: