Пучок прямых
к.ф.-м.н., доцент: Нусь С.Я.
Уфа 2013
Содержание
Уравнение пучка прямых. 3
Задачи. 7
Литература. 10
Уравнение пучка прямых
Всякое уравнение первой степени относительно декартовых координат изображает прямую линию, и обратно, всякая прямая линия изображается в декартовых координатах уравнением первой степени.
Уравнение прямой, разрешенное относительно ординаты 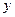 , имеет вид:
, имеет вид:
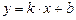 (1)
(1)
Параметр k характеризует направление прямой и называется ее угловым коэффициентом. В случае прямоугольной системы координаты: 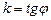 , где
, где 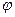 - угол, образованный прямой с положительным направлением оси абсцисс. В случай косоугольной системы координат:
- угол, образованный прямой с положительным направлением оси абсцисс. В случай косоугольной системы координат: 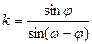
Второй параметр уравнения (1), свободный член b, равен величине отрезка, отсекаемого данной прямой на оси ординат, считая от начала координат.
Если известны угловые коэффициенты 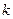 и
и 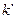 двух прямых, то угол
двух прямых, то угол 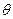 между этими прямыми вычисляется для прямоугольной системы координат и по формуле:
между этими прямыми вычисляется для прямоугольной системы координат и по формуле: 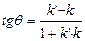 , для косоугольной системы:
, для косоугольной системы: 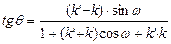
Условие параллельности двух прямых выразится так: 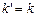
Условие перпендикулярности двух прямых: 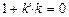
Для прямоугольной системы и для косоугольной системы координат:
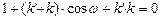 . Прямая, проходящая через точку (
. Прямая, проходящая через точку (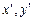 ) и имеющая угловой коэффициент
) и имеющая угловой коэффициент 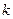 , изображается уравнением:
, изображается уравнением: 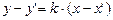
Нормальное уравнение прямой имеет следующий вид: 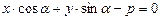 при
при 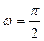 , или в общем виде:
, или в общем виде: 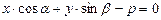 ,
, 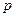 обозначает длин перпендикуляра, опущенного из начала координат на данную прямую (
обозначает длин перпендикуляра, опущенного из начала координат на данную прямую (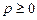 );
); 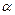 обозначает угол между этим перпендикуляром и положительным направлением оси
обозначает угол между этим перпендикуляром и положительным направлением оси 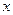 ;
; 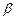 - угол между этим же перпендикуляром и осью
- угол между этим же перпендикуляром и осью 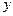 :
: 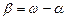
Всякое уравнение первой степени 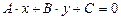 может быть приведено к нормальному виду, для чего достаточно умножить его на нормирующий множитель:
может быть приведено к нормальному виду, для чего достаточно умножить его на нормирующий множитель: 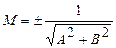 при
при 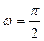 , в общем случай:
, в общем случай: 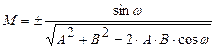 . Нормирующий множитель должен иметь знак, обратный знаку свободного члена
. Нормирующий множитель должен иметь знак, обратный знаку свободного члена 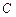 данного уравнения. Если
данного уравнения. Если 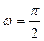 , то параметры соответствующей прямой вычисляются по формулам:
, то параметры соответствующей прямой вычисляются по формулам: 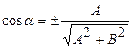 ,
, 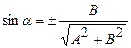 ,
, 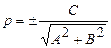 , в случае косоугольной системы координаты:
, в случае косоугольной системы координаты: 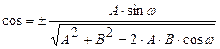 ,
,
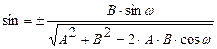 ,
, 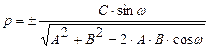 .
.
Расстояние 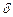 точки
точки 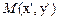 от данной прямой равно абсолютной величине левой части нормального уравнения этой прямой, в которой текущей координаты заменены координатами точки
от данной прямой равно абсолютной величине левой части нормального уравнения этой прямой, в которой текущей координаты заменены координатами точки 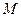 , т.е. в случае прямоугольной системы:
, т.е. в случае прямоугольной системы:
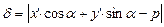 (2)
(2)
в случае косоугольной системы:
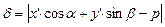 (3)
(3)
Если же прямая дана общим уравнением первой степени 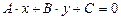 , то его нужно предварительно привести к нормальному виду, и искомое расстояние будет:
, то его нужно предварительно привести к нормальному виду, и искомое расстояние будет:
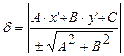 (4)
(4)
или
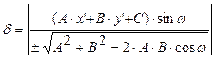 (5)
(5)
Если в формулах (2)-(5) мы отбросим в правых частях знак абсолютной величины, то при вычислениях будем получать число 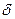 со знаком плюс или минус, в зависимости от того, находится ли точка и начало координат по разные стороны или по одну и ту же сторону от прямой.
со знаком плюс или минус, в зависимости от того, находится ли точка и начало координат по разные стороны или по одну и ту же сторону от прямой.
Исследование общего уравнения прямой: 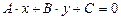 , если
, если 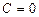 , то прямая проходит через начало координат, если
, то прямая проходит через начало координат, если 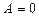 , то прямая параллельна оси абсцисс, если
, то прямая параллельна оси абсцисс, если 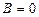 , то прямая параллельна оси ординат, если
, то прямая параллельна оси ординат, если 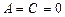 , то прямая совпадает с осью абсцисс, если
, то прямая совпадает с осью абсцисс, если 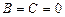 , то прямая совпадает с осью ординат.
, то прямая совпадает с осью ординат.
Если даны две прямые:
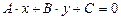 и
и 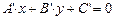 (6)
(6)
угол между ними вычисляется в случае прямоугольной системы координат по формуле: 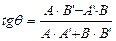 , в случае косоугольной системы:
, в случае косоугольной системы: 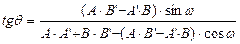 . Условие параллельности прямых для любой системы координат:
. Условие параллельности прямых для любой системы координат: 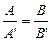 . Условие перпендикулярности прямых:
. Условие перпендикулярности прямых: 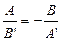 для
для 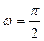 ,
, 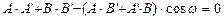 для любого
для любого 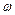 .
.
Чтобы найти координаты точки пересечения двух прямых (26) надо совместно решить их уравнения: 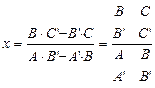 ,
, 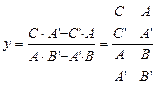 .
.
Если 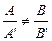 , то прямые имеют определенную точку пересечения. Если
, то прямые имеют определенную точку пересечения. Если 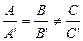 , то прямые параллельны и точки их пересечения нет. Если
, то прямые параллельны и точки их пересечения нет. Если 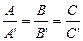 , то прямые совпадают и точка пересечения становится неопределенной.
, то прямые совпадают и точка пересечения становится неопределенной.
Совокупность всех прямых, проходящих через одну и ту же точку, называется пучком прямых, а их общая точка - центром пучка. Если 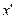 и
и 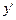 обозначают координаты центра, то уравнение определяет любую прямую пучка.
обозначают координаты центра, то уравнение определяет любую прямую пучка.
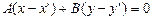 (7)
(7)
Давая отношению 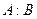 определенное значение, мы выделяем из пучка (7) одну определенную прямую. Центр пучка может быть определен не только своими координатами, но и любыми двумя прямыми, через него проходящими. Если даны две прямые:
определенное значение, мы выделяем из пучка (7) одну определенную прямую. Центр пучка может быть определен не только своими координатами, но и любыми двумя прямыми, через него проходящими. Если даны две прямые: 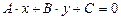 и
и 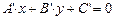 , то всякая прямая, проходящая через их точку пересечения, изобразится уравнением:
, то всякая прямая, проходящая через их точку пересечения, изобразится уравнением: 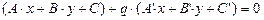 .
.
Каждому значению параметра 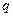 пучка соответствует определенная прямая пучка; меняя
пучка соответствует определенная прямая пучка; меняя 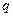 , мы получим всевозможные прямые пучка, определенного двумя основными прямыми (6).
, мы получим всевозможные прямые пучка, определенного двумя основными прямыми (6).

Задачи
№299
Написать уравнение прямой, проходящей через точку пересечения прямых: 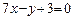 и
и 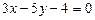 через точку
через точку 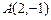 .
.
Решение: Всякая прямая, проходящая через точку пересечения двух данных прямых, изобразится уравнением: 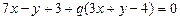 . Нужно только подобрать значение параметра
. Нужно только подобрать значение параметра 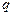 так, чтобы прямая прошла через точку
так, чтобы прямая прошла через точку 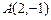 , т.е. чтобы координаты этой точки удовлетворяли уравнению прямой; подставляя их в уравнение пучка:
, т.е. чтобы координаты этой точки удовлетворяли уравнению прямой; подставляя их в уравнение пучка: 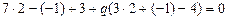 , далее
, далее 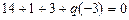
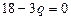 , значит
, значит 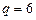 . Подставим
. Подставим 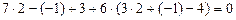 , получаем
, получаем 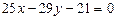 .
.
Ответ: 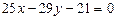
№300
Через точку пересечения прямых 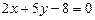 и
и 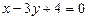 провести прямую, которая, кроме того: 1) проходит через начало координат; 2) параллельна оси абсцисс; 3) параллельна оси ординат; 4) проходит через точку
провести прямую, которая, кроме того: 1) проходит через начало координат; 2) параллельна оси абсцисс; 3) параллельна оси ординат; 4) проходит через точку 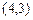 .
.
Решение: Пользуясь уравнением пучка прямых: 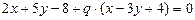
1) Надо брать параметр q так, чтобы свободный член обращался в ноль: 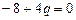 , отсюда
, отсюда 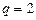 , подставим
, подставим 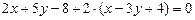 , получим
, получим 
2)параметр q подбирается так, чтобы коэффициент при х обратился в ноль: 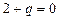 , получим
, получим 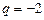 , подставим
, подставим 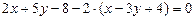 , получим
, получим 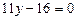
3)параметр q подбирается так, чтобы коэффициент при y обратился в ноль: 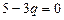 , получим
, получим 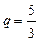 , подставим
, подставим 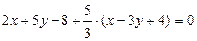 , получим
, получим 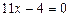
4) параметр q подбирается так, чтобы координаты этой точки удовлетворяли уравнению прямой: 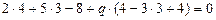 , отсюда
, отсюда 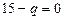 , получим
, получим 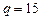 , подставим
, подставим 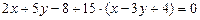 , получим
, получим 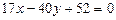
Ответ: 1) 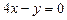 , 2)
, 2) 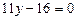 , 3)
, 3) 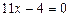 , 4)
, 4) 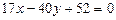
№302
Не вычисляя координат вершин треугольника, написать уравнения прямых, проведенных через эти вершины параллельно противолежащим сторонам. Стороны треугольника даны уравнениями: 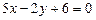 ,
, 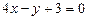 и
и 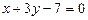 .
.
Решение:Уравнение любой прямой, проходящей через первую вершину, т.е. через точку пересечения двух сторон, будет: 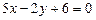 (1). Искомая прямая, проходящая через эту вершину, должна быть параллельно третьей стороне треугольника; следовательно коэффициенты при координатах в их уравнениях должны быть:
(1). Искомая прямая, проходящая через эту вершину, должна быть параллельно третьей стороне треугольника; следовательно коэффициенты при координатах в их уравнениях должны быть: 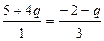 , отсюда
, отсюда 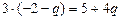 , затем
, затем 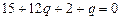 , получим
, получим 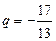 , подставляем в (1)
, подставляем в (1) 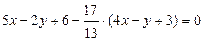 , получим
, получим 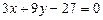 . Прямая, проходящая через вторую вершину:
. Прямая, проходящая через вторую вершину: 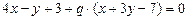 , следовательно коэффициенты при координатах в их уравнениях должны быть:
, следовательно коэффициенты при координатах в их уравнениях должны быть: 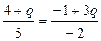 , отсюда
, отсюда 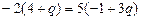 , получим
, получим 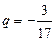 , подставляем в (1):
, подставляем в (1): 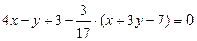 , получим
, получим 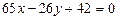 . Прямая, проходящая через третью вершину:
. Прямая, проходящая через третью вершину: 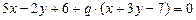 , следовательно коэффициенты при координатах в их уравнениях должны быть:
, следовательно коэффициенты при координатах в их уравнениях должны быть: 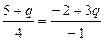 , отсюда
, отсюда 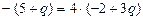 , получим
, получим 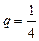 , подставляем в (1) получим:
, подставляем в (1) получим: 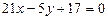 Ответ:
Ответ: 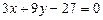 ,
, 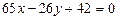 и
и 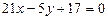
Литература
1. Бортяковский, А.С. Аналитическая геометрия в примерах и задачах: Учеб. пособие/ А.С. Бортаковский, А.В. Пантелеев.- М.: Высш. шк., 2005.- 496 с.: ил.- (Прикладная математика).- ISBN: 5-06-004761- Х.
2. Канатников, А.Н., Крищенко, А.П. Аналитическая геометрия: Учеб. Для вузов. 2- е изд. /Под ред. В.С. Зарубина, А.П. Крищенко.- М.: Издательство МГТУ им. Н.Э. Баумана, 2000.-388 с.: ил.- (Математика в техническом университете).- ISBN: 5-7038-1671-8.
3. Резниченко, С.В. Аналитическая геометрия в примерах и задачах: М.: Издательство МФТИ, 2001.- 576 с.- ISBN: 5-89155-062-8.
4. Цубербиллер, О. Н. Задачи и упражнения аналитической геометрии. – 33- е изд., стер.- СПб.: Издательство «Лань», 2007.- 336с.: ил.- (Учебник для вузов).- ISBN: 978-5-8114-0475-9.
 2015-06-28
2015-06-28 2374
2374