Рассмотрим решение задач

1. Постройте график функции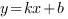, если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.

В уравнении функции 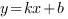два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.

а) Из того, что график функции 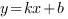параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид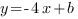

б) Нам осталось найти b. Известно, что график функции 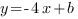проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:

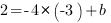отсюда b=-10

Таким образом, нам надо построить график функции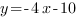

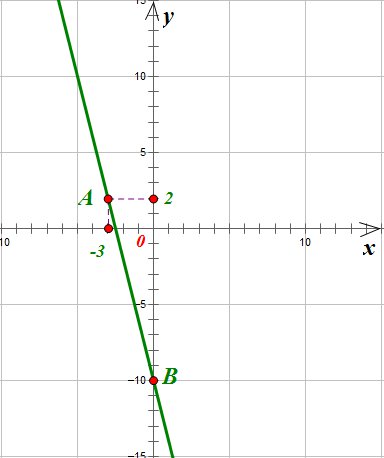
Точка А(-3;2) нам известна, возьмем точку B(0;-10)

Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).

Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой 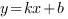. То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение 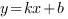и получим систему линейных уравнений.

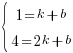
Вычтем из второго уравнения системы первое, и получим 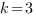. Подставим значение k в первое уравнение системы, и получим b=-2.

Итак, уравнение прямой .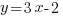

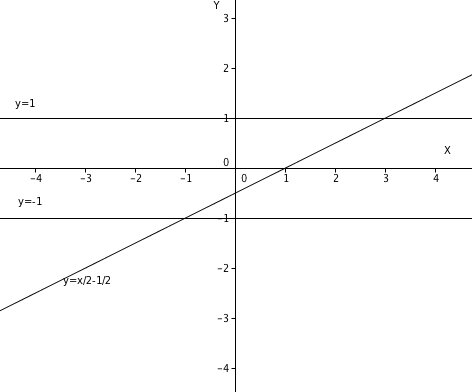
3. Постройте график уравнения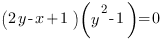

Чтобы найти, при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учестьОДЗ каждого множителя.

Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:

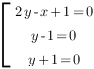
Построим графики всех уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения :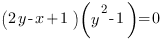

4. Постройте график функции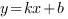, если он перпендикулярен прямой 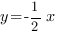и проходит через точку М(-1;2)

Мы не будем строить график, только найдем уравнение прямой.

а) Так как график функции 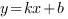, если он перпендикулярен прямой 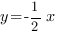, следовательно 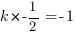, отсюда 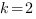. То есть уравнение функции имеет вид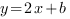

б) Мы знаем, что график функции 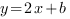проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:

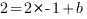, отсюда .

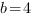Следовательно, наша функция имеет вид: .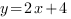

5. Постройте график функции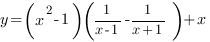

Упростим выражение, стоящее в правой части уравнения функции.

Важно! Прежде чем упрощать выражение, найдем его ОДЗ.

Знаменатель дроби не может быть равен нулю, поэтому 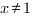-1″ title=»x<>-1″/> .

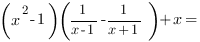
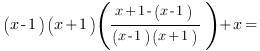
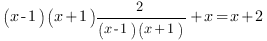
Тогда наша функция принимает вид:

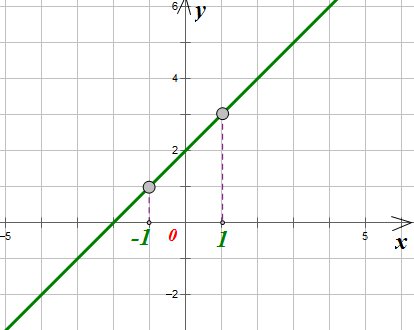
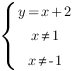и выколоть на нем две точки: с абсциссами x=1 и x=-1: