2015-06-28
524
Згинання стрижня буде косим у випадках, коли площина дії зовнішніх сил не збігається з головними площинами.
Косе згинання зручно представляти у вигляді суми двох прямих згинань. Для цього згинаючий момент М розкладається на складові моменти відносно головних осей поперечного перерізу u і v.
Згідно з принципом незалежності дії сил, прогини і напруження при косому згині визначаються геометричним складанням відповідних складових від дії двох прямих згинань.
У лабораторній роботі використовується стрижень, поперечний переріз якого є рівнобічним кутником. Кінець стрижня В защемлений між захватами випробної машини Р-5, а кінець А навантажений зосередженою силою Р,яка з головними площинами стрижня становить кут 45°. Складов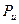і 
, і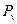 
сили Р по головних осях u і v перерізу однакові й дорівнюють 0,707 Р (рис. 9.1). Тому й епюри згинаючих моментів 
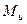і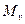 
теж будуть однаковими.
Розрахункові значення прогинів перерізу С балки в напрямі головних осей и і v мажна визначити за методом Мора, перемножуючи відповідні епюри по правилу Верещагіна:
; 
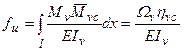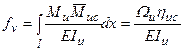(9.1)
де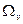 
, 
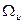- значення площ епюр 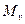та ;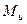 
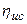- значення 
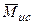під центром площі епюри 
; 
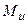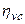- значення 
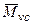під центром площі епюри 
.
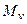Повний прогин перерізу С дорівнює:
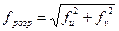. (9.2)
Напруження у довільній точці К перерізу D балки дорівнює:
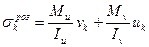, (9.3)
тут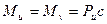 
- згинаючі моменти; 
, 
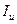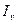- моменти інерції перерізу відносно головних осей; 
, 
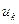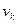- координати точки К відносно головних осей и і v.
Щоб експериментально визначити напруження у точці К перерізу D, використовується тензометр.
Експериментальне значення прогину перерізу С виражається через вертикальний та горизонтальний прогини, що вимірюються індикаторами годинникового типу.
При випробуванні на косе згинання стрижня кутового перерізу слід мати на увазі, що центр його згинання не збігається з центром перерізу. Тому, для виключення впливу закручування, зміщення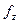 
і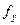 
потрібно вимірювати для центру згинання, який розміщується у точці N перетину осей полиць кута.
