· Скалярным произведением векторов 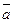 и
и 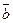 называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 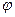 между ними:
между ними:
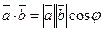 .
.
В частном случае 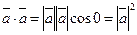 или
или 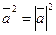 .
.
· Свойства:
1) 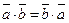 ;
;
2) 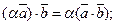
3) 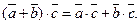
· Скалярное произведение можно выразить через проекции 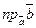
(проекцию вектора 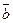 на вектор
на вектор 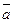 ) или
) или 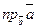 (проекцию вектора
(проекцию вектора 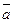 на вектор
на вектор 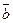 ):
):
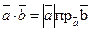 или
или 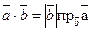 .
.
· Если известны координаты векторов 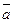 =
= 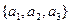 и
и 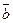 =
= 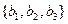 в прямоугольной системе координат, то
в прямоугольной системе координат, то 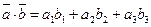 .
.
· Векторным произведением векторов 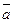 и
и 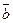 называется вектор (обозначается
называется вектор (обозначается 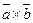 ), перпендикулярный
), перпендикулярный 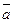 и
и 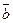 , направленный так, что тройка векторов
, направленный так, что тройка векторов 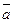 ,
, 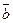 ,
, 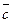 ─ правая,модуль которого
─ правая,модуль которого 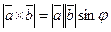 .
.
В частном случае 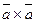 =
= 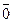 .
.
Упорядоченная тройка векторов называется правой, если направление векторов определяется правилом правой руки (правилом буравчика).
Свойства:
1) 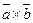 =
= 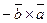 ;
;
2) 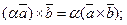
3) 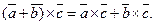
Если известны координаты векторов 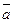 =
= 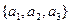 ,
, 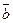 =
= 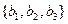 в прямоугольной системе координат, то
в прямоугольной системе координат, то
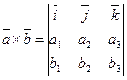 .
.
· Смешанным произведением векторов 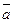 ,
, 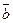 ,
, 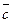 называется скалярное произведение одного из этих векторов на векторное произведение двух других векторов (обозначается
называется скалярное произведение одного из этих векторов на векторное произведение двух других векторов (обозначается 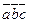 ).
).
Если известны координаты векторов 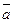 =
= 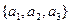 ,
, 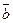 =
= 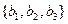 ,
, 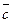 =
= 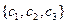 в прямоугольной системе координат, то
в прямоугольной системе координат, то
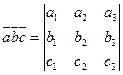 .
.
 2015-06-28
2015-06-28 202
202







