Базисом лінійного простору є впорядкована множина, яка містить максимально можливу кількість лінійно незалежних векторів цього простору.
Будемо розглядати базиси скінченого лінійного простору 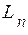 , які складаються з одиничних векторів,
, які складаються з одиничних векторів,
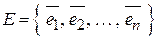 .
.
Теорема про розклад вектора. Будь-який вектор 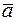 єдиним чином можна представити як лінійну комбінацію базисних векторів
єдиним чином можна представити як лінійну комбінацію базисних векторів
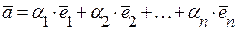 .
.
Числа 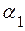 ,
, 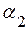 , …,
, …, 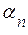 (
(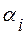 – альфа
– альфа 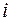 -ті) називають координатами вектора
-ті) називають координатами вектора 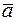 в даному базисі
в даному базисі 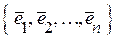 і пишуть
і пишуть 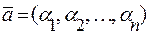 .
.
Ця властивість лінійного простору дозволяє представляти просторові (геометричні) вектори у алгебраїчній формі, тобто геометричним об’єктам 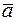 єдиним чином співставляти алгебраїчні об’єкти в заданому базисі лінійного простору
єдиним чином співставляти алгебраїчні об’єкти в заданому базисі лінійного простору 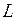 ,
,
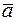
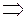
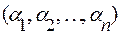 .
.
Зауваження. Змінивши базис одержимо інший впорядкований набір чисел, який буде визначати координати того самого вектора в новому базисі:
вектор 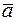 у базисі
у базисі 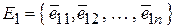
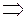
 ,
,
вектор 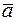 у базисі
у базисі 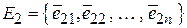
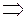
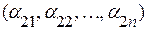 ,
,
причому, якщо 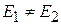 , то
, то 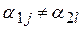 ;
; 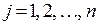 ;
; 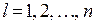 .
.
Наприклад. Розглянемо одновимірний лінійний простір 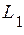 . Виберемо у якості базисного одиничний вектор
. Виберемо у якості базисного одиничний вектор 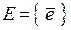 . Вектор
. Вектор 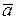 належить простору,
належить простору, 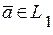 , тому
, тому 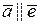 . Координата вектора
. Координата вектора 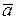 в базисі
в базисі 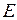 дорівнює довжині вектора
дорівнює довжині вектора 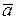 і є додатною, якщо вектор
і є додатною, якщо вектор 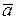 співнапрямлений базисному вектору
співнапрямлений базисному вектору 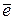 або від’ємною, якщо вектор
або від’ємною, якщо вектор 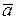 протилежно напрямлений вектору
протилежно напрямлений вектору 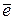 :
:
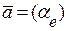 ,
, 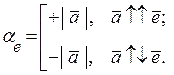
Якщо змінити базисний вектор 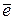 , на вектор
, на вектор 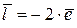 ,
, 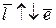 , то в новому базисі
, то в новому базисі 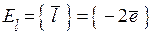 основна кількісна характеристика вектора
основна кількісна характеристика вектора 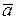 , якою є його довжина, зберігається. Знак координати вектора
, якою є його довжина, зберігається. Знак координати вектора 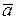 в новому базисі
в новому базисі 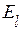 показує чи співпадають напрями векторів, чи ні. Модуль координати визначає в скільки разі довжина вектора
показує чи співпадають напрями векторів, чи ні. Модуль координати визначає в скільки разі довжина вектора 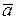 відрізняється від довжини базового вектора
відрізняється від довжини базового вектора 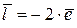 .
.
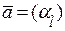 ,
, 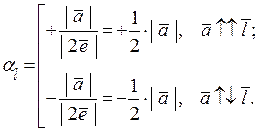
Представлення векторів у координатній формі дає можливість вивчати властивості векторів та дій з векторами методами алгебри.
Далі вектори будемо розглядати як впорядковані набори чисел 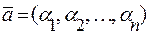 , які відповідають координатам вектора у заданому базисі
, які відповідають координатам вектора у заданому базисі 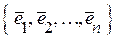 лінійного простору
лінійного простору 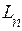 .
.
Приклад 1. Кожний вектор 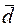 паралельний деякій прямій
паралельний деякій прямій 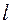 ,
, 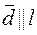 , можна розкласти за базисом
, можна розкласти за базисом 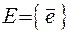 на цій прямій. Завжди знайдеться таке число
на цій прямій. Завжди знайдеться таке число 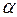 , що
, що  . Очевидно, що
. Очевидно, що
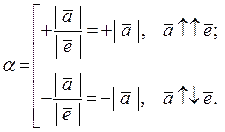
Приклад 2. Кожний вектор паралельний деякій площині можна розкласти за базисом цієї площини. Прикладом розкладу у фізиці є розклад сили, на дві складові. Якщо базисні вектори неперпендикулярні, то складові розкладу сили можна знайти, побудувавши паралелограм на базисних векторах 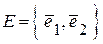 співнапрямлених з її складовими
співнапрямлених з її складовими 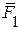 та
та 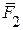 ,
, 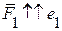 ,
, 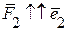 . Вектор, який дорівнює рівнодійній
. Вектор, який дорівнює рівнодійній 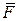 відповідає діагоналі паралелограма. Складові рівнодійної
відповідає діагоналі паралелограма. Складові рівнодійної 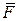 будуть дорівнювати:
будуть дорівнювати:
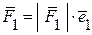 ,
, 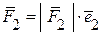
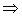
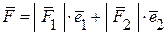 .
.
Приклад 3. Кожний вектор можна розкласти за базисом у просторі 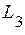 . Для будь-якого вектора
. Для будь-якого вектора 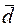 і некомпланарних векторів
і некомпланарних векторів 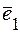 ,
, 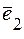 ,
, 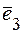 знайдуться такі числа
знайдуться такі числа 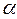 ,
, 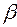 ,
, 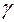 , що
, що 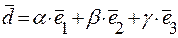 . Складові
. Складові 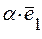 ,
, 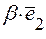 ,
, 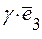 можна знайти за правилом паралелограма.
можна знайти за правилом паралелограма.
В л а с т и в о с т і в е к т о р і в
з а д а н и х у к о о р д и н а т н і й ф о р м і
Розглянемо властивості векторів заданих у координатній формі в одному і тому самому базисі 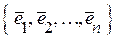 лінійного простору
лінійного простору 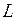 .
.
1. Рівність векторів. Два вектори 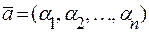 і
і 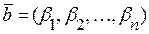 рівні тоді і тільки тоді, коли рівні їх відповідні координати в одному і тому самому базисі лінійного простору
рівні тоді і тільки тоді, коли рівні їх відповідні координати в одному і тому самому базисі лінійного простору 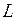 :
: 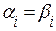 ;
; 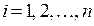 . Це випливає з єдиності розкладання вектора за заданим базисом лінійного простору.
. Це випливає з єдиності розкладання вектора за заданим базисом лінійного простору.
2. Паралельність векторів. Два вектори 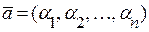 і
і
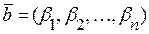 колінеарні тоді і тільки тоді, коли їх відповідні координати пропорційні:
колінеарні тоді і тільки тоді, коли їх відповідні координати пропорційні: 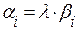 ,
, 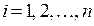 .
.
Наприклад. Колінеарними є вектори 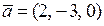 і
і 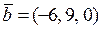 , оскільки їх координати пропорційні,
, оскільки їх координати пропорційні, 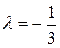 ,
,
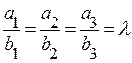
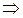
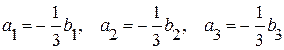 ,
,
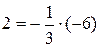 ,
, 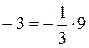 ,
, 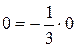 .
.
Оскільки коефіцієнт пропорційності 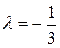 , то вектор
, то вектор 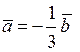 , тобто вектори
, тобто вектори 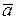 і
і 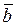 протилежно напрямлені,
протилежно напрямлені, 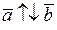 . Довжина вектора
. Довжина вектора 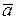 втричі менша за довжину вектора
втричі менша за довжину вектора 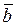 ,
, 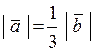 .
.
Так як вектори 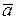 і
і 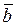 паралельні їх можна розмістити на одній прямій. Ці вектори є лінійно залежними.
паралельні їх можна розмістити на одній прямій. Ці вектори є лінійно залежними.
3. Компланарність векторів. Три вектори компланарні 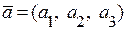 ,
, 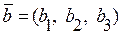 ,
, 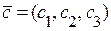 тоді і тільки тоді, коли визначник, побудований на координатах цих векторів, дорівнює нулю
тоді і тільки тоді, коли визначник, побудований на координатах цих векторів, дорівнює нулю
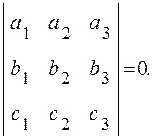
Наприклад. 1. Для того, щоб з’ясувати, чи є вектори 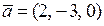 ,
, 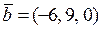 ,
, 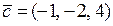 компланарними, обчислимо їх визначник,
компланарними, обчислимо їх визначник,
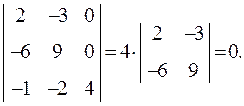
Вектори 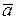 ,
, 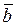 ,
, 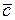 лежать у одній площині. Ці вектори є лінійно залежними.
лежать у одній площині. Ці вектори є лінійно залежними.
2. Чи є вектори 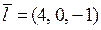 ,
, 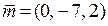 ,
, 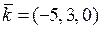
лінійно залежними? Перевіримо ці вектори на компланарність. Складемо визначник,
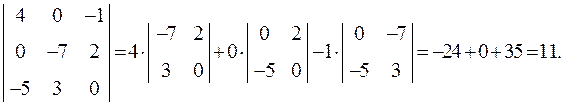
Вектори 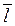 ,
, 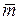 ,
, 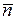 не лежать у одній площині, тобто вони лінійно незалежні.
не лежать у одній площині, тобто вони лінійно незалежні.
Завдання для самостійної роботи
1. Визначити графічно складові вектора 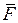 , який є рівнодійною сил
, який є рівнодійною сил 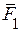 та
та 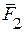 . Рівнодійну силу та напрями її складових задати самостійно.
. Рівнодійну силу та напрями її складових задати самостійно.
2. Розкласти геометричний вектор 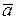 , заданий у базисі
, заданий у базисі 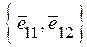 ,
, 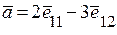 , у новому базисі
, у новому базисі 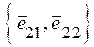 . Вектор
. Вектор 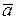 та напрями базисних векторів вибрати самостійно. Розклади вектора за базисами зобразити графічно. Записати вектор
та напрями базисних векторів вибрати самостійно. Розклади вектора за базисами зобразити графічно. Записати вектор 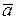 у координатній формі в кожному з базисів.
у координатній формі в кожному з базисів.
3. Визначити, які з векторів є колінеарними: 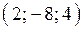 ,
, 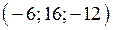 ,
, 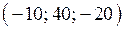 .
.
4. Визначити, яка з сукупностей містить компланарні вектори:
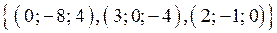 ;
; 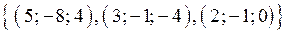 ;
;
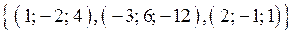 ;
; 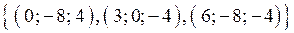 .
.
Пояснити, чому вектори у сукупності є лінійно залежними.
Питання для самоперевірки
 2015-06-28
2015-06-28 4000
4000







