Def 1. Двойное векторное произведение векторов 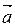 ,
, 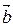 ,
, 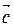 это произведение вида
это произведение вида 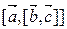 .
.
Выразим двойное векторное произведение через скалярное.
Пусть 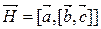 Þ
Þ 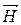 ^
^ 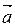 и
и 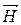 ^
^ 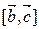 . Тогда, в силу
. Тогда, в силу 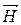 ^
^ 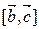 Þ
Þ  лежит в плоскости векторов
лежит в плоскости векторов 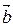 и
и 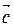 Þ
Þ 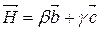 . Умножим это равенство скалярно на
. Умножим это равенство скалярно на 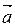 . Имеем
. Имеем 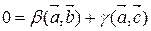 .
.
Пусть вектор 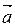 не перпендикулярен одновременно векторам
не перпендикулярен одновременно векторам 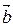 и
и 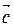 (в противном случае
(в противном случае 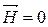 в обоих случаях). Тогда
в обоих случаях). Тогда 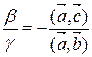 Þ
Þ 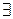
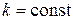 , такое что
, такое что 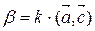 ,
, 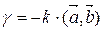 .
.
Тогда
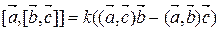 .
.
Для того, чтобы найти 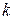 , вычислим левую и правую части в некотором базисе. Пусть вектор
, вычислим левую и правую части в некотором базисе. Пусть вектор 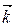 направлен вдоль вектора
направлен вдоль вектора 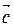 ,
, 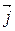 лежит в плоскости векторов
лежит в плоскости векторов 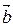 и
и 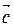 ,
, 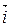 определяется из условия, что
определяется из условия, что 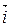 ,
, 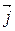 ,
, 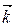 образуют правую тройку. Тогда
образуют правую тройку. Тогда 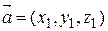 ,
, 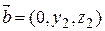 ,
, 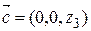 .
.
Имеем
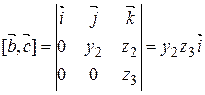 ,
, 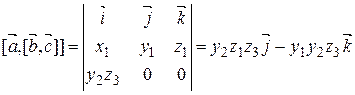 .
.
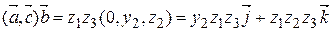 .
.
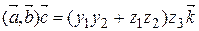 .
.
Отсюда видно, что 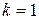 . Итак, справедлива формула:
. Итак, справедлива формула:
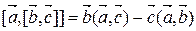 .
.
Пример 1. Доказать тождество Якоби:
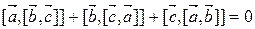 .
.
Имеем
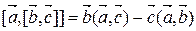 ,
,
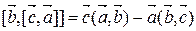 ,
,
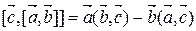 .
.
Суммируя эти равенства, получим тождество Якоби.
Пример 2. Вычислить 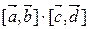 .
.
Имеем: (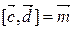 )
) 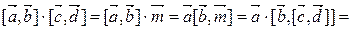
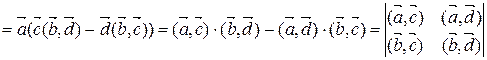 .
.
 2015-06-28
2015-06-28 278
278






