Задача 23
Задан многочлен 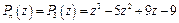 ;
;
а) найти корни многочлена;
б) разложить многочлен по корням;
в) разложить многочлен на множители только с действительными коэффициентами.
а) 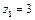 ; разделим
; разделим 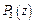 на
на 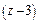 :
:
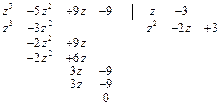
рассм. теперь ур – е 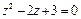 ;
; 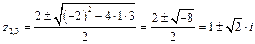 ;
;
б) разложение многочлена 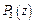 на линейные множители:
на линейные множители:
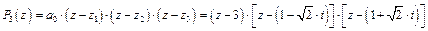 ;
;
разложение многочлена 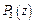 на множители только с действительными коэффициентами:
на множители только с действительными коэффициентами:
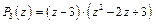 .
.
Задача 24(а)
Установить вид и построить линию, заданную уравнением: 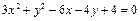 .
.
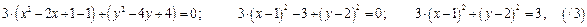
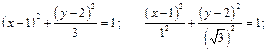 - эллипс с центром в точке
- эллипс с центром в точке 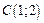 и полуосями
и полуосями 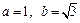 .
.
Задача 25
Привести уравнение поверхности 2-го порядка к каноническому виду, определить вид поверхности.
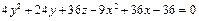 ;
;
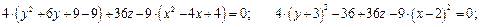
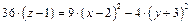 ;
; 
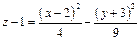 ;
;
перейдём к новым координатам по формулам: 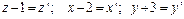 ;
;
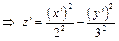 , - гиперболический параболоид.
, - гиперболический параболоид.
Задача 26 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей
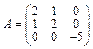 .
.
1) Находим собств. значения 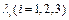 линейного преобразования
линейного преобразования 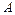 , т.е. корни характеристического уравнения
, т.е. корни характеристического уравнения 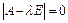 :
:
рассм. 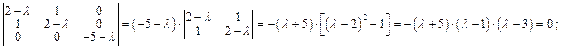
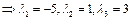 - собств. значения (действ. и различные) лин. преобр-я
- собств. значения (действ. и различные) лин. преобр-я  ;
;
2) находим собств. векторы линейного преобразования  , соотв. собств. значениям
, соотв. собств. значениям  :
:
а) рассм. 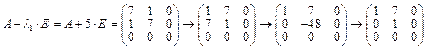 ;
;
рассм. 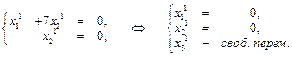 пусть
пусть 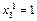 , тогда вектор
, тогда вектор 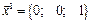 ;
;
б) рассм. 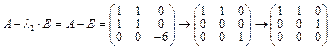 ;
;
рассм. 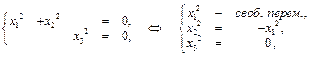
пусть 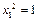 , тогда
, тогда 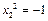 ,
,  вектор
вектор 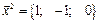 ;
;
в) рассм. 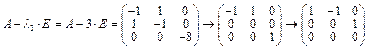 ;
;
рассм. 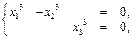
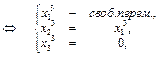
пусть 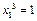 , тогда
, тогда 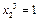 ,
,  вектор
вектор 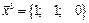 ;
;
след. собств. векторы линейного преобразования 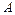 суть:
суть: 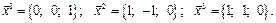
 2015-06-28
2015-06-28 151
151






