| Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. |
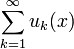
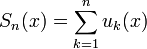 — n-ная частичная сумма.
— n-ная частичная сумма.
[править] Сходимость
Ряд называется сходящимся поточечно, если последовательность 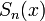 его частичных сумм сходится поточечно.
его частичных сумм сходится поточечно.
Ряд называется сходящимся поточечно, если последовательность 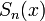 его частичных сумм сходится равномерно.
его частичных сумм сходится равномерно.
[править] Необходимое условие равномерной сходимости
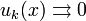
[править] Критерий Коши равномерной сходимости
Критерий Коши для последовательности 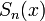 . Чтобы последовательность функций
. Чтобы последовательность функций 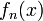 , определенных на множестве V, равномерно сходилась на этом множестве, необходимо и достаточно, чтобы для всякого ε > 0 существовал номер N = N (ε), такой, что при всех n, m больше либо равных N одновременно для всех
, определенных на множестве V, равномерно сходилась на этом множестве, необходимо и достаточно, чтобы для всякого ε > 0 существовал номер N = N (ε), такой, что при всех n, m больше либо равных N одновременно для всех 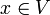 выполнялось неравенство
выполнялось неравенство 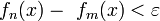
[править] Абсолютная и условная сходимость
Ряд 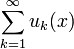 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если 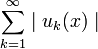 сходится. Абсолютно сходящийся ряд сходится.
сходится. Абсолютно сходящийся ряд сходится.
Если ряд 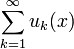 сходится, а
сходится, а 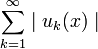 расходится, то ряд
расходится, то ряд 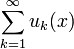 называется сходящимся условно. Для таких рядов верна теорема Римана о перестановке членов условно сходящегося ряда.
называется сходящимся условно. Для таких рядов верна теорема Римана о перестановке членов условно сходящегося ряда.
[править] Признаки равномерной сходимости
[править] Признак сравнения
Ряд 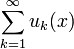 сходится абсолютно и равномерно, если выполнены условия:
сходится абсолютно и равномерно, если выполнены условия:
1. Ряд 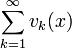 сходится равномерно.
сходится равномерно.
2. 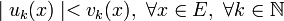
Частным случаем является признак Вейерштрасса, когда 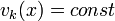 . Таким образом функциональный ряд ограничиваеся обычным. От него требуется обычная сходимость
. Таким образом функциональный ряд ограничиваеся обычным. От него требуется обычная сходимость
[править] Признак Дирихле
Ряд 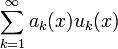 сходится равномерно, если выполнены следующие условия:
сходится равномерно, если выполнены следующие условия:
1. Последовательность действительнозначных функций 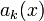 монотонна
монотонна 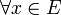 и
и 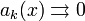
2. Частичные суммы 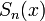 ряда
ряда 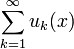 равномерно ограничены.
равномерно ограничены.
[править] Признак Абеля
Ряд 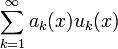 сходится равномерно, если выполнены следующие условия:
сходится равномерно, если выполнены следующие условия:
1. Последовательность действительнозначных функций 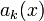 равномерно ограничена и монотонна
равномерно ограничена и монотонна 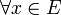 .
.
2. Ряд 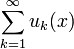 равномерно сходится.
равномерно сходится.
2 [править]Свойства равномерно сходящихся последовательностей и рядов
[править] Теоремы о непрерывности
Рассматриваются комплекснозначные функции на множестве 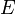
Последовательность непрерывных в точке функций сходится к функции непрерывной в этой точке.
Последовательность 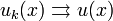
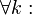 функция
функция 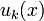 непрерывна в точке
непрерывна в точке 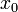
Тогда 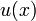 непрерывна в
непрерывна в 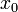 .
.
Ряд непрерывных в точке функций сходится к функции непрерывной в этой точке.
Ряд 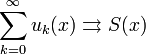
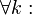 функция
функция 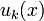 непрерывна в точке
непрерывна в точке 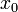
Тогда 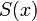 непрерывна в
непрерывна в 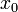 .
.
[править] Теоремы об интегрировании
Рассматриваются действительнозначные функции на отрезке действительной оси.
Теорема о переходе к пределу под знаком интеграла.
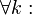 функция
функция 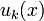 непрерывна на отрезке
непрерывна на отрезке 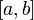
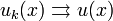 на
на 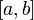
Тогда 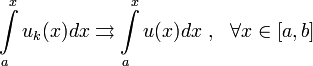
Теорема о почленном интегрировании.
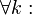 функция
функция 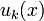 непрерывна на отрезке
непрерывна на отрезке 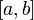
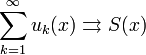 на
на 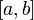
Тогда 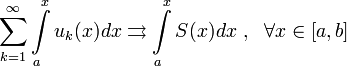
[править] Теоремы о дифференцировании
Рассматриваются действительнозначные функции на отрезке действительной оси.
Теорема о дифференцировании под пределом.
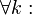 функция
функция 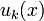 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 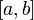
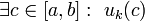 сходится
сходится
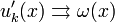 на отрезке
на отрезке 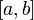
Тогда 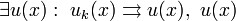 — непрерывно дифференцируема на
— непрерывно дифференцируема на 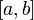 ,
, 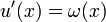 на
на 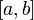
Теорема о почленном дифференцировании.
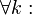 функция
функция 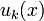 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 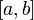
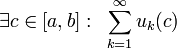 сходится
сходится
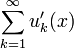 равномерно сходится на отрезке
равномерно сходится на отрезке 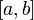
Тогда 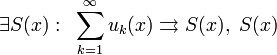 — непрерывно дифференцируема на
— непрерывно дифференцируема на 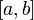 ,
, 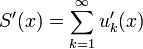 на
на 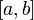
 2015-06-24
2015-06-24 240
240






