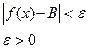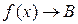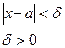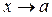Лекція № 24
Тема: Границя функції.
1. Поняття про границю функції.
2. Основні теореми про границі. Неперервність функції в точці.
3. Поняття невизначеності, способи її розкриття.
Поняття про границю функції
В загальному випадку 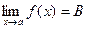 означає: якщо
означає: якщо 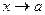 , то
, то 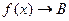
|
|
|
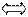
|
Число В називається границею функції при х, що прямує до а, якщо для будь-якого додатного числа e знайдеться таке додатне число d, що при всіх х¹а, які задовольняють нерівність 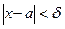 виконується нерівність
виконується нерівність 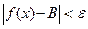 .
.
Якщо границя існує 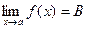 , то вона – єдина.
, то вона – єдина.
Теореми про границі. Неперервність функції в точці
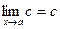 | 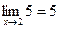 | |
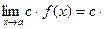 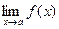 | 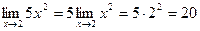 | |
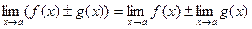 | 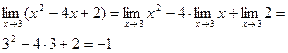 | |
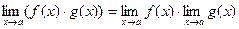 | 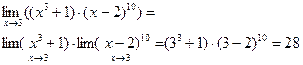 | |
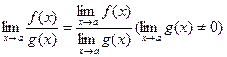 | 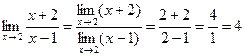 |
Наслідки
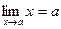 , а – будь-яке , а – будь-яке | |
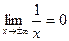 | |
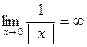 | |
Якщо 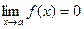 і і 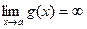 , то , то 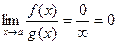 | |
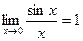 - чудова границя - чудова границя |
Поняття невизначеності, способи її розкриття.
Якщо при підстановці х= а, отримали 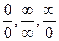 , то ця
, то ця
ситуація називається – н евизначеність. Її потрібно розкривати
за правилами:
1. Розкласти чисельник та знаменник на множники та
скоротити;
2. Якщо дріб не скорочується, то чисельник та знаменник
домножити на вираз спряжений до знаменника(чи чисельника),
а потім скоротити.
3. Якщо під знаком границі стоять тригонометричні функції чи
обернені тригонометричні функції, то зводимо до першої
визначеної границі.
 2015-06-28
2015-06-28 831
831