1. Даны точки Р (– 2; 3; 4); Q (1; – 4; 5), R (3; –6; 7).
Для них: а) найти координаты векторов 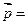
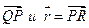 ;
;
б) найти координаты вектора  ;
;
в) вычислить длину вектора 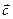 ;
;
г) найти модули и направляющие косинусы векторов 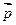 и
и 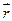 .
.
2. Даны точки А (– 2; 1; 3); В (5; – 3; 6), С (1; 0; –2), D(4; – 7; – 1).
Для них: а) найти координаты векторов 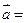
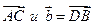 ;
;
б) найти координаты вектора 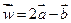 и его длину
и его длину 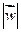 ;
;
в) найти координаты вектора 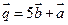 и его модуль
и его модуль 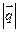 ;
;
г) найти направляющие косинусы векторов 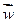 и
и 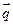 .
.
3. Проверить, образуют ли векторы 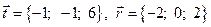 и
и 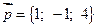 базис.
базис.
(Указание: проверить, являются ли они линейно-независимыми, и сравнить количество векторов с количеством координат).
4. Проверить на линейную зависимость векторы 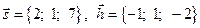 и
и 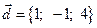 .
.
5. Вектор 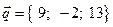 разложить по базису
разложить по базису 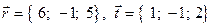 ,
, 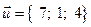
6. Дана тройка векторов 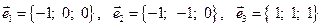 . Убедиться, что они образуют базис, и найти разложение вектора
. Убедиться, что они образуют базис, и найти разложение вектора 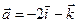 по этому базису.
по этому базису.
7. Найти разложение вектора 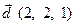 по базису векторов
по базису векторов 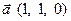 ,
, 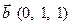 и
и 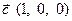 .
.
8. Даны векторы 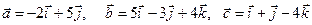 . Найти координаты вектора
. Найти координаты вектора 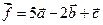 .
.
9. Даны точки A (1, – 2,3), B (3, 2, 1) и C (6, 4, 4) и D(4; 0; 6). Для них:
а) найти координаты векторов 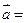
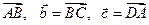 ;
;
б) проверить на коллинеарность векторы 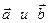 ;
;
в) проверить на коллинеарность векторы 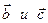 .
.
10. При каком t векторы 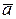 =
= 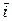 + t
+ t 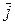 –
– 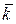 и
и 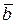 = 3
= 3 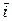 + 6
+ 6 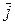 – 3
– 3 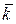 коллинеарны?
коллинеарны?
11. Даны вектора 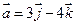 ;
; 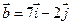 и
и 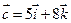 . Для них:
. Для них:
а) вычислить 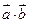 ;
;
б) вычислить 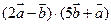 ;
;
в) найти косинус угла φ между векторами 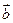 и
и 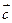 .
.
12. Даны точки N (2; 1; 0); P (– 1; – 3; 4), R (– 5; 3; 1), T (1; – 2; 2).
Для них: а) найти координаты векторов 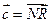 ;
; 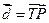 и
и 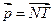 ;
;
б) вычислить косинус угла φ между векторами 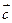 и
и 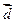 ;
;
в) вектора 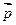 и
и 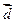 проверить на перпендикулярность.
проверить на перпендикулярность.
13. При каком 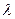 вектора
вектора 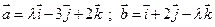 являются взаимно перпендикулярными?
являются взаимно перпендикулярными?
14. Векторы 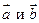 составляют угол
составляют угол 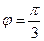 . Известно, что
. Известно, что 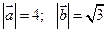 . Вычислить значения скалярных произведений
. Вычислить значения скалярных произведений 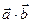 и
и 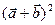 .
.
15. Найти проекцию вектора 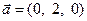 на направление вектора
на направление вектора 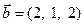 .
.
16. Найти проекцию вектора 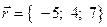 на ось, составляющую с координатными осями равные острые углы.
на ось, составляющую с координатными осями равные острые углы.
17. Вектор 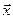 коллинеарен вектору
коллинеарен вектору 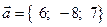 . Дан вектор
. Дан вектор 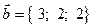 и известно, что
и известно, что 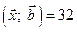 . Найти координаты вектора
. Найти координаты вектора 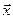 .
.
18. Даны векторы 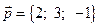 и
и 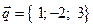 . Найти вектор
. Найти вектор 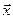 , перпендикулярный оси
, перпендикулярный оси 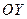 , и удовлетворяющий условиям
, и удовлетворяющий условиям 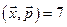 и
и 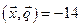 .
.
19. Даны вектора 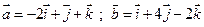 ,
, 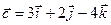 .
.
Для них вычислить: а) 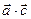 и
и 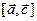 ;
;
б) 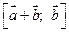 ;
;
в) 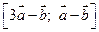 ;
;
г) 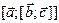 .
.
20. Даны векторы 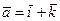 и
и 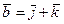 . Вычислить модуль векторного произведения
. Вычислить модуль векторного произведения 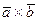 .
.
21. Дан треугольник с вершинами А (1; – 1; 2), В (5; – 6; 2) и С (1; 3;–1). Найти: 1) площадь треугольника АВС; 2) длину высоты, опущенной из т. С на сторону АВ.
22. Даны вершины параллелограмма A(1, –2, 3), B(3, 2, 1), C(6, 4, 4) и D(4; 0; 6). Найти длину высоты, опущенной из т. В на сторону СD.
23. Найти синус угла между векторами 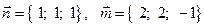 .
.
24. Вычислить смешанное произведение векторов 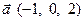 ,
, 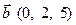 и
и 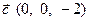 .
.
25. Даны точки А(2; – 1; 1); В(5; 5; 4), С(3; 2; –1), D(4; 1; 3). Проверить, лежат ли эти точки в одной плоскости.
26. Установить, компланарны ли вектора 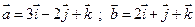 и
и 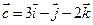 .
.
27. Найти объем параллелепипеда, построенного на векторах 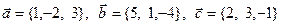 .
.
28. Даны вершины тетраэдра P (1; 1; –1), Q (2; 3; 1), R (3; 2; 1), S (5, 9, –9). Найти длину его высоты, опущенной из вершины Q.
29. Вектор 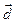 перпендикулярен векторам
перпендикулярен векторам 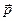 и
и 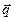 . Угол между
. Угол между 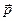 и
и 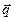 равен
равен 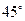 . Зная, что
. Зная, что 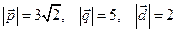 , найти
, найти 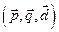 .
.
ОТВЕТЫ К ЗАДАЧАМ:
1. а) 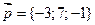 ,
, 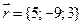 ; б)
; б) 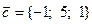 ; в)
; в) 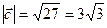 ; г) для
; г) для 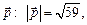
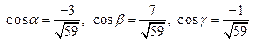 ; для
; для 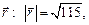
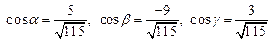 .
.
2. а) 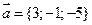 ,
, 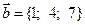 ; б)
; б) 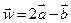
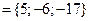 и
и 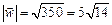 ;
;
в) 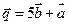
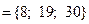 и
и 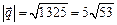 ; г)
; г) 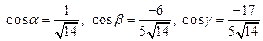 ;
;
д) 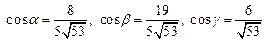 .
.
3. Нет, векторы не образуют базис, т.к. линейно зависимы.
4. Векторы линейно независимы.
5. 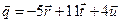 .
.
6. 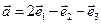 .
.
7. 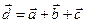 .
.
8. 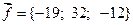 .
.
9. а) 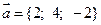 ,
, 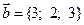 ,
, 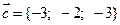 ; б)
; б) 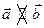 ; в)
; в) 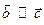 .
.
10. t = 2.
11. а) 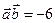 ; б)
; б) 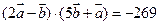 ; в)
; в) 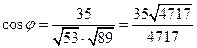 .
.
12. а) 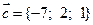 ,
, 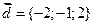 ,
, 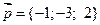 ; б)
; б) 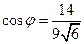 ; в) не перпендикулярны.
; в) не перпендикулярны.
13. 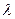 = – 6.
= – 6.
14. 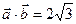 и
и 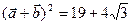 ;
;
15. 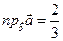 .
.
16. 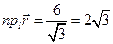 .
.
17. 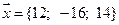 .
.
18. 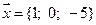 .
.
19. а) 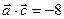 и
и 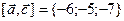 ; б)
; б) 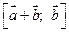 =
= 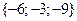 ; в)
; в) 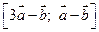 =
= 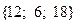 ;
;
г) 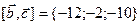 и
и 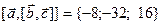 .
.
20. 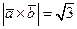 .
.
21. а) 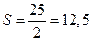 ; б)
; б) 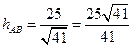 .
.
22. 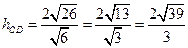 .
.
23. 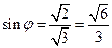 .
.
24. 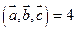 .
.
25. Точки не лежат в одной плоскости.
26. Вектора не компланарны.
27. 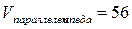 .
.
28. 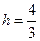 .
.
29. 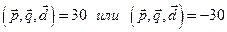 .
.
 2015-06-28
2015-06-28 263
263






