2015-06-28
705
Однородное разрешающее уравнение для основного напряженного состояния круговой цилиндрической оболочки имеет вид [1, 3]
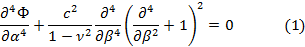
где Ф(α,β) – разрешающая функция,
h, R – толщина и радиус оболочки,
α, β - безразмерные координаты,
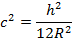
ν – коэффициент Пуассона.
Перемещения, усилия и изгибающие моменты связаны с Ф(α,β) соотношениями:
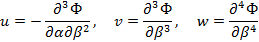
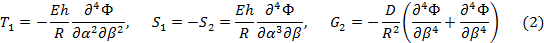
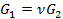
Здесь D – цилиндрическая жесткость.
Б) Решение разрешающего дифференциального уравнения
Представим функцию Ф(α,β) в виде одинарного тригонометрического ряда
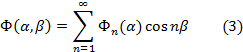
-3-
а выражения для искомых факторов (2) в виде следующих рядов:
;
;
;
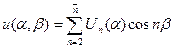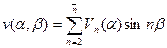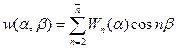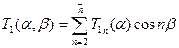; (4)
.
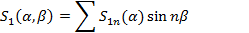
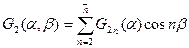Подставляя (3) в (1), получим вместо дифференциального уравнения в частных производных обыкновенное дифференциальное уравнение для n -го члена ряда
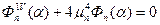(5)
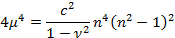
Решение обыкновенного дифференциального уравнения (5) имеет вид
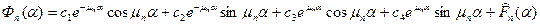(6)
где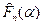 
- частное решение соответствующее действующей на оболочку нагрузке.
Перепишем решение (6) в другом виде, а именно через гиперболо-тригонометрические функции:
|
|
|
,
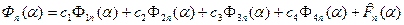
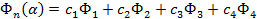где
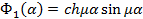
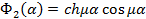(7)
- 4-
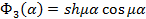
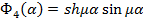
c1, c2, c3, c4 –произвольные постоянные; (8)
В (7) индекс “n” у функций Ф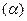 
опущен.
В результате подстановки (3), (4) в (2) получаем связь между амплитудными значениями искомых факторов и разрешающей функции, а именно:
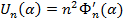
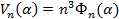
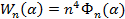(9)
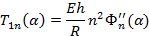
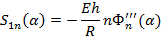
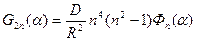
Как показано в работах В.З. Власова [1], весьма эффективным при расчете оболочек является метод начальных параметров (МНП). Математической основой для МНП служит решение известной задачи Коши.
Произвольные постоянные (8) выражаются через значения искомых факторов в некотором начальном сечении, где они принимают название начальных параметров. За такое сечение здесь принимается координата одного из двух краев оболочки: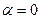 
. Это позволяет, исходя из краевых условий в начальном сечении, которые известны заранее, определить два начальных параметра (они, как правило, равны нулю) и затем получить два алгебраических уравнения, вытекающих из формулирования краевых условий на другом конце оболочки (
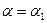) относительно оставшихся двух начальных параметров. Таким образом, краевая задача приводится к решению двух, вместо четырех, алгебраических уравнений для нахождения двух начальных параметров.
С помощью метода начальных параметров построено решение для круговой цилиндрической оболочки, загруженной в сечении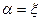 
-5-
радиальной сосредоточенной в продольном направлении силой Pγ [2]. Оно представлено в таблице 1.
Таблица 1
| 
| 
| 
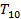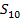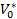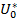| Правая часть | ||
- n 
| ||||||
| 
| 
| 
| 
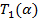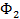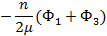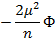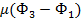| KTS(α-ξ) | |
| 
|
| 
| 
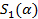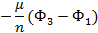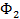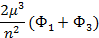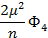| KSS(α-ξ) | |
| 
| 
|
| 
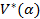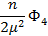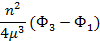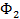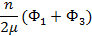| KVS(α-ξ) | |
| 
| 
| 
|
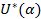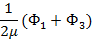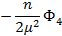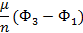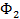| KUS(α-ξ) |
Примечание:
1) 
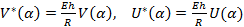; индексы “n” у искомых факторов функций Ф, у коэффициента 
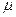опущены.
|
|
|
2) 
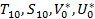- начальные параметры, то есть значения этих функций в избранном начальном сечении, здесь 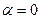. 3)
3) Подстрочный индекс «n» опущен.
В правой части таблицы представлены частные решения при действии силы Pγ., для которой коэффициент разложения нагрузки в ряд Фурье находится по формуле:
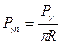
Заметим, что функции влияния, стоящие в правой части таблицы 1, отличны от нуля только 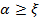при 
; при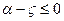 
вместо этого аргумента
-6-
следует подставлять значение 0 (ноль) и при нем определять значение функции Ф.
В случае действия кусочно-постоянной вдоль части образующей оболочки [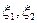 
] нагрузки, в правой части таблицы 1 - в результате использования этого решения в качестве функции Грина - интегрированием по указанной области [ 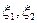] получаются следующие выражения для частных решений 
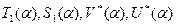, которые следует вставить в таблицу1 взамен её правой части:
Таблица 2 (правая часть к таблице 1)
- 
|
|
|
|
|
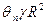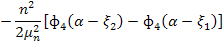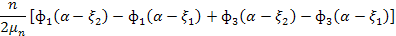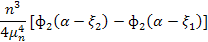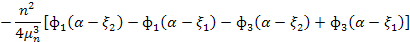В таблице 2 через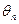 
обозначены коэффициенты ряда Фурье действующей нагрузки.
В случае действия нагрузки, постоянной вдоль всей образующей оболочки [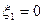 
. 
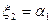], как это имеет место в данном задании, в правой части таблицы получаются следующие выражения для частных решений 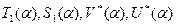, как частный случай таблицы 2:
-7-
Таблица 3 (частный случай таблицы 2 при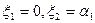 
)
| -
|
 
|
|
|
|
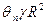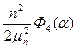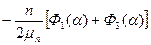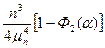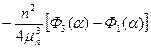Таким образом, при действующем давлении жидкости правая часть
таблицы 1 должна быть заменена только что приведенной таблицей 3.
В) Разложение гидростатической нагрузки в ряд Фурье по косинусам
Подчеркнем, что выражения для искомых амплитудных значений в таблице находятся для n-го члена ряда, начиная с n=2 (n =2, 3, 4, ….), и в соответствии с этим в виде ряда должна быть представлена действующая гидростатическая нагрузка (*):
; (
)
;
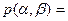
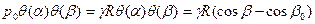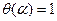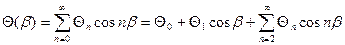где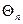 
- коэффициенты ряда Фурье.
-8-
Здесь первые два члена ряда (n=0, n=1), в общем случае, соответствуют деформированию оболочки как жесткого целого, без изменения формы поперечного кругового сечения, то есть она ведет себя как стержень при n=0 и как балка при n =1.
В данном конкретном случае как стержень она не нагружена, и напряжения равны нулю. Решение для n = 1 получаются по формулам сопромата, а в данном случае - по справочнику.
Найдем коэффициенты ряда Фурье функции нагрузки
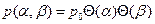, в которой по определению :
;
; 
;
;
.
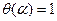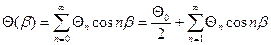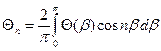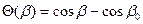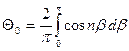
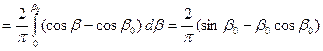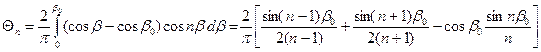Г) Пример.
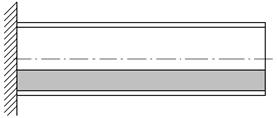
Пусть имеется сосуд с маргинальными условиями на краях: один жестко защемленный, другой свободный, как показано на рисунке. Тогда в случае применения уравнений обшей теории оболочек краевые условия должны быть сформулированы следующим образом:
Левый край,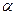 
= 0: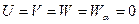 
Правый край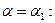 
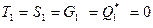
В теории основного состояния, где применяются уравнения модифицированной полубезмоментной теории, как мы видим, имеется возможность удовлетворить лишь по два граничных условия на каждом крае, как это показано на рисунке.
Краевые условия:
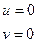
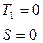
-9-
Оставшиеся краевые условия могут быть удовлетворены на основе применения метода асимптотического синтеза напряженного состояния с помощью уравнений краевого эффекта [3], и здесь не рассматриваются.
Список литературы
1. Власов В.З. Общая теория оболочек и ее применение в технике.- М.,
Изд - во АН СССР, том 1, 1962. 528 с.
2. Власов В.З. Тонкостенные пространственные системы. М., Госстройиздат,
1958. 502 с. (Изд - во АН СССР, том 3, 1962)
3. Нерубайло Б.В. Локальные задачи прочности цилиндрических оболочек.
М., «Машиностроение», 1983. 248 с.
