Краткие теоретические сведения
При анализе сложных электротехнических устройств иногда полезно представить отдельные блоки сложных устройств в виде простых четырехполюсников, а затем преобразовать их совокупность в эквивалентный четырехполюсник. Возможны пять комбинаций соединений выводов четырехполюсников.
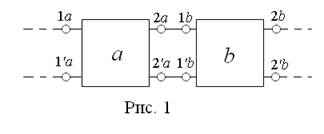
Соединение (рис.1), при котором выходы первого четырехполюсника(a) соединены с соответствующими входами второго (b), называется каскадным. При каскадном соединении входное напряжение четырехполюсника b – U 1 b поступает с выхода первого четырехполюсника, т.е. равно 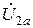 . Выходной ток
. Выходной ток 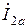 создает входной ток
создает входной ток 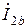 . Следовательно, для построения эквивалента нужна система параметров, в которой напряжение и ток относятся к одной группе выводов. Этому требованию удовлетворяют системы А- параметров.
. Следовательно, для построения эквивалента нужна система параметров, в которой напряжение и ток относятся к одной группе выводов. Этому требованию удовлетворяют системы А- параметров.
В А- уравнениях истоками являются выходные напряжение и ток, 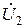 и
и 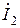 , а стоками – входные величины
, а стоками – входные величины 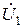 и
и 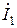 . В результате
. В результате 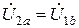 ,
, 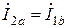 .
.
С учётом приведённых граничных условий получим уравнения эквивалентного четырёхполюсника:
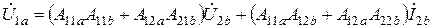 ;
;
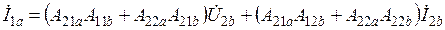 .
.
Такая структура коэффициентов соответствует произведению двух А- матриц, поэтому перепишем уравнения в матричной форме:
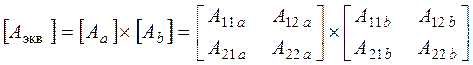 . (1)
. (1)
Таким образом, при каскадном соединении четырехполюсников нужно использовать систему А -параметров и находить А- параметры эквивалента как произведение А- параметров составляющих. Это правило распространяется на любое количество каскадно-соединенных четырехполюсников.
Соединение, приведенное на рис. 2, называется последовательным. Это связано с тем, что:
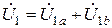 ;
; 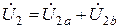 ;
; 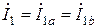 ;
; 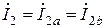 ,
,
а равенство токов элементов и суммирование их напряжений – это признак последовательного соединения.
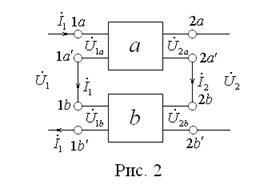
Для схемы (рис. 2) истоками являются токи 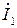 и
и 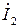 , а стоками –
, а стоками – 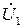 и
и 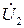 , поэтому естественно в этом случае применить Z- матрицу.
, поэтому естественно в этом случае применить Z- матрицу.
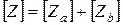 (2)
(2)
Для схемы, изображенной на рис. 3, имеем:
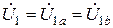 ;
; 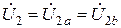 ;
; 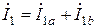 ;
; 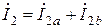 ,Токи суммируются при параллельном соединении. Истоками являются напряжения
,Токи суммируются при параллельном соединении. Истоками являются напряжения 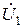 и
и 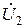 , а стоками –
, а стоками – 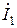 и
и 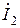 .
.
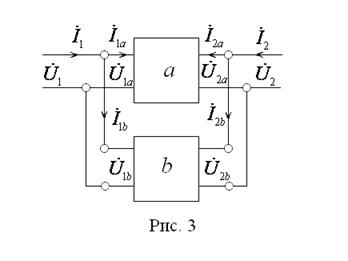
Очевидно, что в этом случае:
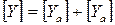 (3)
(3)
поэтому при параллельном соединении используются Y- параметры, причем Y -матрица эквивалентного четырехполюсника образована суммой Y- параметров составляющих.
В схеме (рис. 4):
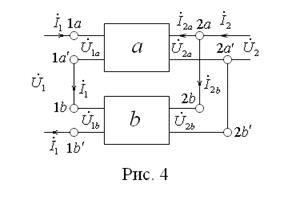
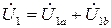 ;
; 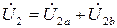 ;
; 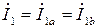 ;
; 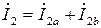 .
.
Такое соединение называется последовательным по входу и параллельным по выходу. Легко показать, что в этом случае нужно применить гибридные Н -параметры:
[ Н ] = [ Нa ]+[ Нb ]. (4)
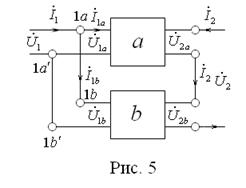
В соединении, параллельном по входу и последовательном по выходу (рис. 5): [ G ]=[ Ga ]+[ Gb ]. (5)
 2015-06-24
2015-06-24 2022
2022