В методах прямого поиска мы не имели никакой информации о минимизируемой функции за исключением ее значений в выбранных нами точках и предположения, что она непрерывна и является унимодальной функцией на рассматриваемом отрезке. Если функцию в некоторой окрестности точки ее минимума можно достаточно точно заменить (аппроксимировать) многочленом, то для ее минимизации целесообразно использовать так называемые методы полиномиальной аппроксимации. Их общая особенность состоит в вычислении коэффициентов многочлена по известным значениям функции в отдельных точках и последующем нахождении минимума этого многочлена с использованием необходимых и достаточных условий экстремума. Ограничимся рассмотрением метода квадратичной аппроксимации минимизируемой функции f (x), в котором график этой функции приближенно заменяют параболой, проходящей через три известные точки [ х i, fi), i = 1, 2, 3, где fi= f (xi).
Известно…, что через три различные точки, не лежащие на одной прямой, можно провести только одну параболу у = ах 2 + b х + с, a ≠ 0. Коэффициенты а, b, с удовлетворяют системе линейных алгебраических уравнений (СЛАУ)
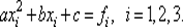
Определитель этой СЛАУ

представляет собой определитель Вандермонда и отличен от нуля, когда х 1, х 2, х 3попарно различны. В этом случае СЛАУ имеет решение, и притом единственное. Его можно записать в виде
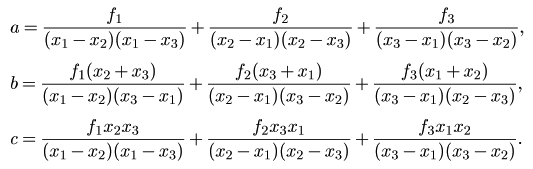
Если найденные выражения для коэффициентов а и b подставить в необходимое условие у ' = 2 ах + b = 0 экстремума функции, то получим ее единственную стационарную точку
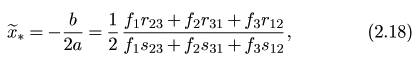
где 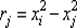 и sij= xi– xj. i, j = 1, 2, 3. Так как у " = 2 а = const, то в точке
и sij= xi– xj. i, j = 1, 2, 3. Так как у " = 2 а = const, то в точке 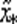 при а > 0 имеем минимум функции у (х), а при a < 0 — максимум.
при а > 0 имеем минимум функции у (х), а при a < 0 — максимум.
Если известен отрезок, на котором минимизируемая функция унимодальна, то нет необходимости вычислять значение коэффициента а. Достаточно этот отрезок принять в качестве отрезка [ x 1, x 3], а точку х 2∈ (x 1, x 3) выбрать произвольно в интервале (x 1, x 3). В этом случае имеем f 1≥ f 2и f 3≥ f 2, откуда 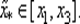
На первом шаге метода квадратичной аппроксимации при помощи (2.18) вычисляют 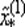 и затем
и затем 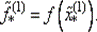 Для вычислений на втором шаге из четырех точек
Для вычислений на втором шаге из четырех точек 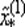 и xi, i = 1, 2, 3, выбирают новую тройку точек
и xi, i = 1, 2, 3, выбирают новую тройку точек 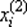 по следующему правилу:
по следующему правилу:
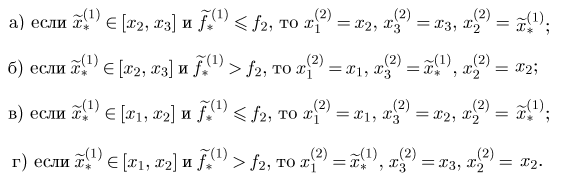
Далее из (2.18) находят 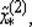 а затем описанную процедуру повторяют на третьем шаге и так далее до тех пор, пока длина интервала неопределенности, в котором гарантированно лежит искомая точка x *минимума функции f (x), не станет меньше заданного наибольшего допустимого значения ε *. Отметим, что подтверждением приближения к точке x *и правильности вычислений может служить уменьшение значения функции у (x) в найденной точке
а затем описанную процедуру повторяют на третьем шаге и так далее до тех пор, пока длина интервала неопределенности, в котором гарантированно лежит искомая точка x *минимума функции f (x), не станет меньше заданного наибольшего допустимого значения ε *. Отметим, что подтверждением приближения к точке x *и правильности вычислений может служить уменьшение значения функции у (x) в найденной точке 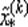 по сравнению со значением
по сравнению со значением 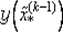 на предыдущем шаге.
на предыдущем шаге.
Пример 2.5. Применим описанную модификацию метода квадратичной аппроксимации для нахождения минимума функции
f (x) = (x – 1)2(x – 3)2
на отрезке [2, 8]. График этой функции приведен на рис. 2.12. Процесс итераций закончим, если длина интервала неопределенности не будет превышать 0.15. На первом шаге выберем 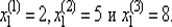 Результаты вычислений с учетом (2.19) сведены в табл. 2.6.
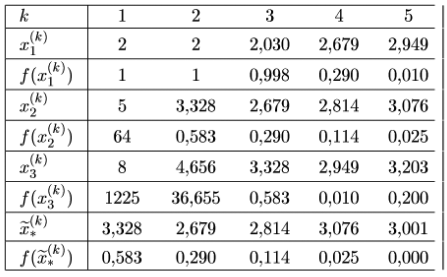
Результаты вычислений с учетом (2.19) сведены в табл. 2.6.
После выполнения пятого шага приходим к заключению, что точка х *минимума функции f (x) расположена в интервале (2,949, 3,076) длины 0,127. Точное значение х *= 3 соответствует минимальному значению f (x *) = 0.
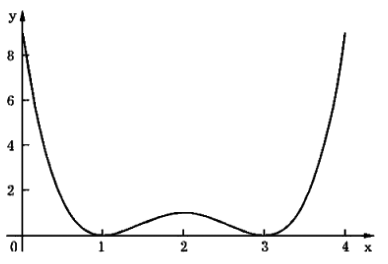
Рис. 2.12
Таблица 2.6
 2015-06-24
2015-06-24 4214
4214








