- Понятие первообразной функции.
- Неопределенный интеграл.
- Свойства неопределенного интеграла.
- Интегралы основных элементарных функций.
- Независимость вида неопределенного интеграла от выбора аргумента.
- Замена переменой в неопределенном интеграле.
- Интегрирование по частям.
- Постановка задачи интегрирования в конечном виде.
- Интегрирование интегралов вида
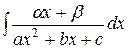 ,
, 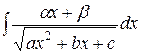 .
. - Интегрирование рациональных выражений.
- Интегрирование тригонометрических выражений.
- Интегрирование некоторых иррациональных выражений.
- Определенный интеграл. Определение, геометрический смысл.
- Свойства определенного интеграла.
- Теорема о среднем.
- Теорема о производной определенного интеграла с переменным верхним пределом.
- Формула Ньютона-Лейбница.
- Классы интегрируемых функций.
- Замена переменной в определенном интеграле. Примеры.
- Формула интегрирования по частям в определенном интеграле. Примеры.
- Несобственные интегралы с бесконечными пределами. Примеры.
- Теоремы о сходимости несобственных интегралов с бесконечными пределами. Примеры.
- Несобственные интегралы от неограниченных функций. Примеры.
- Теоремы о сходимости несобственных интегралов от неограниченных функций. Примеры.
- Площадь плоской фигуры в прямоугольных декартовых координатах. Примеры.
- Площадь плоской фигуры в полярных координатах. Примеры.
- Длина дуги в прямоугольных декартовых координатах. Примеры.
- Длина дуги, заданной в параметрическом виде, в прямоугольных декартовых координатах. Примеры.
- Длина дуги в полярных координатах. Примеры.
- Вычисление объема тела по известным поперечным сечениям.
- Объем тела вращения.
- Площадь поверхности вращения.
- Функции многих переменных. Основные понятия и определения.
- Непрерывность функции двух переменных.
- Приращение функции двух переменных. Частные производные 1 порядка.
- Геометрический смысл частной производной.
- Полный дифференциал функции двух переменных. Геометрический смысл дифференциала функции двух переменных.
- Производные сложной функции двух переменных.
- Неявная функция и ее дифференцирование.
- Касательная плоскость к поверхности.
- Нормаль к поверхности.
- Геометрический смысл полного дифференциала функции двух переменных.
- Повторное дифференцирование функции двух переменных.
- Экстремум функции двух переменных.
- Производная по направлению.
- Градиент.
Примеры экзаменационных задач:
Найти неопределенный интеграл: 1. 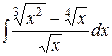 2. 2. 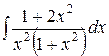 3.
3. 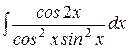 4. 4. 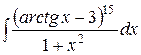 5. 5. 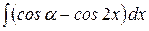 6.
6. 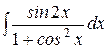
|
Вычислить: а) 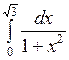 ; б) ; б) 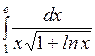 ; в) ; в) 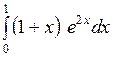
|
Вычислить: а) 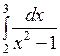 ; б) ; б) 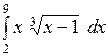 ; в) ; в) 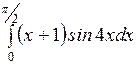
|
Вычислить: а) 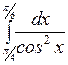 ; б) ; б) 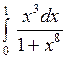 ; в) ; в) 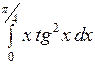
|
Вычислить: а) 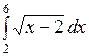 ; б) ; б) 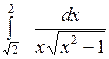 ; в) ; в) 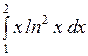
|
Вычислить: а) 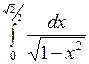 ; б) ; б) 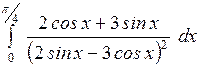 ; в) ; в) 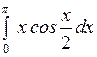
|
Вычислить: а) 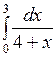 ; б) ; б) 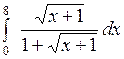 ; в) ; в) 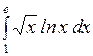
|
Вычислить: а) 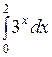 ; б) ; б) 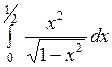 ; в) ; в) 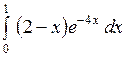
|
Вычислить: а) 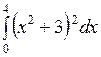 ; б) ; б) 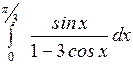 ; в) ; в) 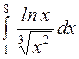
|
Вычислить: а) 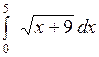 ; б) ; б) 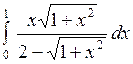 ; в) ; в) 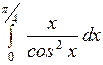
|
Вычислить: а) 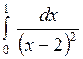 ; б) ; б) 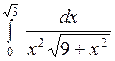 ; в) ; в) 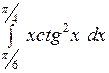
|
Вычислить или установить расходимость: а) 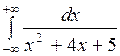 ; б) ; б) 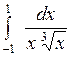
|
Вычислить или установить расходимость: а) 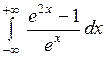 ; б) ; б) 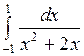
|
Вычислить или установить расходимость: а) 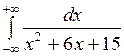 ; б) ; б) 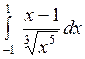
|
Вычислить или установить расходимость: а) 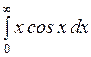 ; б) ; б) 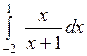
|
Вычислить или установить расходимость: а) 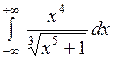 ; б) ; б) 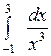
|
Вычислить или установить расходимость: а) 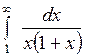 ; б) ; б) 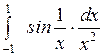
|
Вычислить или установить расходимость: а) 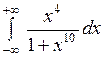 ; б) ; б) 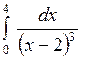
|
Вычислить или установить расходимость: а) 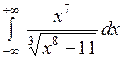 ; б) ; б) 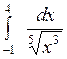
|
Вычислить или установить расходимость: а) 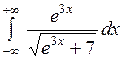 ; б) ; б) 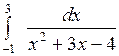
|
Вычислить или установить расходимость: а) 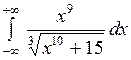 ; б) ; б) 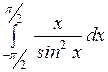
|
Какой из интегралов больше: a) 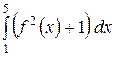 или или 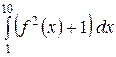 ;
b) ;
b) 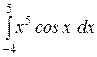 или или 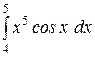 ; c) ; c) 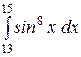 или или 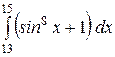 ? ?
|
Какой из интегралов больше: 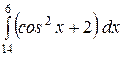 или или 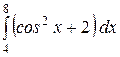 ;
b) ;
b) 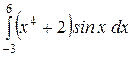 или или 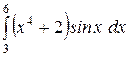 ; c) ; c) 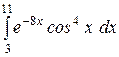 или или 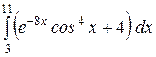 ? ?
|
Какой из интегралов больше: 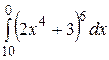 или или 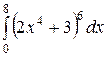 ;
b) ;
b) 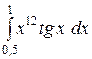 или или 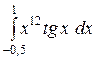 ; c) ; c) 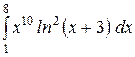 или или 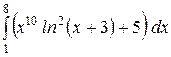 ? ?
|
Какой из интегралов больше: 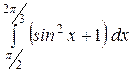 или или 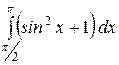 ;
b) ;
b) 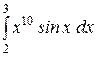 или или 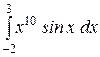 ; c) ; c) 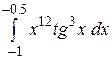 или или 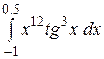 ? ?
|
Какой из интегралов больше: 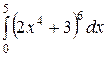 или или 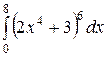 ;
b) ;
b) 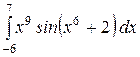 или или 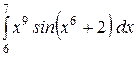 ; c) ; c) 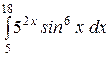 или или 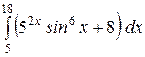 ? ?
|
Какой из интегралов больше: 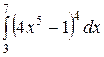 или или 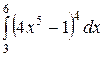 ;
b) ;
b) 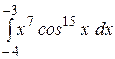 или или 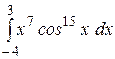 ; c) ; c) 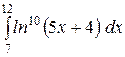 или или 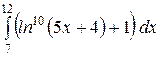 ? ?
|
Вычислить площадь фигуры, ограниченной данными линиями: 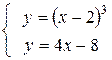
|
Вычислить площадь фигуры, ограниченной данными линиями: 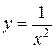 , , 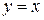 , , 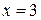
|
Вычислить площадь фигуры, ограниченной данными линиями: 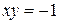 , , 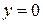 , , 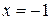 , , 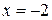
|
Вычислить площадь фигуры, ограниченной данными линиями: 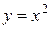 , , 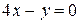
|
Вычислить площадь фигуры, ограниченной данными линиями: 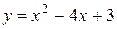 , , 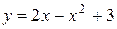
|
Вычислить площадь фигуры, ограниченной данными линиями: 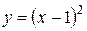 , , 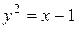
|
Вычислить площадь фигуры, ограниченной данными линиями: 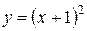 , , 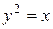 , , 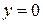 , , 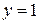
|
Вычислить площадь фигуры, ограниченной данными линиями: 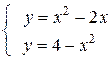
|
Вычислить площадь фигуры, ограниченной данными линиями: 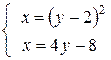
|
Вычислить площадь фигуры, ограниченной данными линиями: 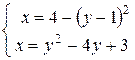
|
Вычислить объем тела, образованного вращением вокруг оси ОХ плоской фигуры, ограниченной линиями: 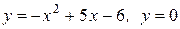
|
Вычислить объем тела, образованного вращением вокруг оси ОУ плоской фигуры, ограниченной линиями: 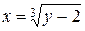 , , 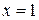 , , 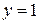
|
Вычислить объем тела, образованного вращением вокруг оси ОХ плоской фигуры, ограниченной линиями: 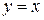 , , 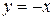 , , 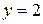
|
Вычислить объем тела, образованного вращением вокруг оси ОУ плоской фигуры, ограниченной линиями: 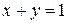 , , 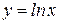 , , 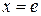
|
Вычислить объем тела, образованного вращением вокруг оси ОХ плоской фигуры, ограниченной линиями: 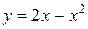 , , 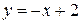
|
Вычислить объем тела, образованного вращением вокруг оси ОУ плоской фигуры, ограниченной линиями: 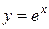 , , 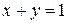 , , 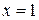
|
Вычислить объем тела, образованного вращением вокруг оси ОХ плоской фигуры, ограниченной линиями: 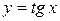 , , 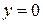 , , 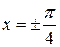
|
Вычислить объем тела, образованного вращением вокруг оси ОУ плоской фигуры, ограниченной линиями: 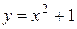 , , 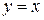 , , 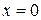 , , 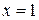
|
Вычислить объем тела, образованного вращением вокруг оси ОХ плоской фигуры, ограниченной линиями: 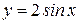 , , 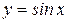 , , 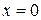 , , 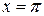
|
Вычислить объем тела, образованного вращением вокруг оси ОУ плоской фигуры, ограниченной линиями: 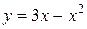 , , 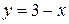 , , 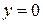
|
Вычислить длину дуги кривой 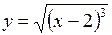 от от 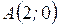 до до 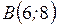
|
Вычислить длину дуги кривой 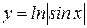 , , 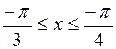
|
Вычислить длину дуги кривой 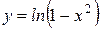 , , 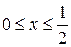
|
Вычислить длину дуги кривой 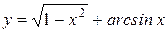 , , 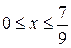
|
Вычислить длину дуги кривой 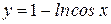 , , 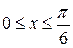
|
Вычислить длину дуги кривой 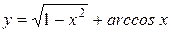 , , 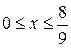
|
Вычислить длину дуги кривой 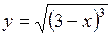 от от 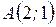 до до 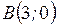
|
Вычислить длину дуги кривой 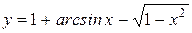 , , 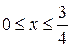
|
Вычислить длину дуги кривой 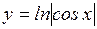 , , 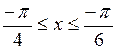
|
Вычислить длину дуги кривой 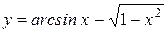 , , 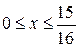
|
Найти уравнения касательной плоскости и нормали к поверхности 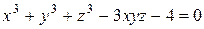 в точке в точке 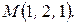
| |||
Найти уравнения касательной плоскости и нормали к поверхности 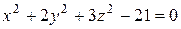 в точке А в точке А 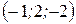 . .
| |||
Найти уравнения касательной плоскости и нормали к поверхности 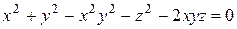 в точке А в точке А 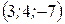 . .
| |||
Найти уравнения касательной плоскости и нормали к поверхности 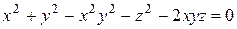 в точке А в точке А 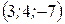 . .
| |||
Найти уравнения касательной плоскости и нормали к поверхности 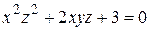 в точке А в точке А 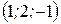 . .
| |||
Найти уравнения касательной плоскости и нормали к поверхности 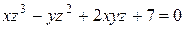 в точке А в точке А 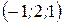 . .
| |||
Найти уравнения касательной плоскости и нормали к поверхности 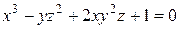 в точке А в точке А 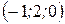 . .
| |||
Найти уравнения касательной плоскости и нормали к поверхности 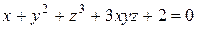 в точке А в точке А 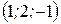 . .
| |||
Найти уравнения касательной плоскости и нормали к поверхности 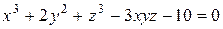 в точке в точке 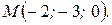
| |||
Найти уравнения касательной плоскости и нормали к поверхности 2 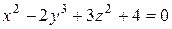 в точке А в точке А 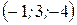 . .
|
Проверить, удовлетворяет ли функция 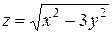 уравнение уравнение 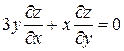
| |||
Проверить, удовлетворяет ли функция 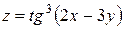 уравнение уравнение 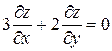 ? ?
| |||
Проверить, удовлетворяет ли функция 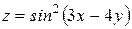 уравнение уравнение 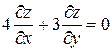
| |||
Проверить, удовлетворяет ли функция 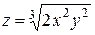 уравнение уравнение 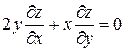
| |||
Проверить, удовлетворяет ли функция 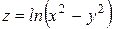 уравнение уравнение 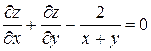
| |||
Проверить, удовлетворяет ли функция 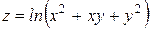 уравнение уравнение 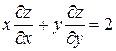
| |||
Проверить, удовлетворяет ли функция 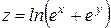 уравнение уравнение 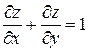
| |||
Проверить, удовлетворяет ли функция 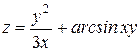 уравнение уравнение 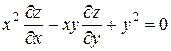
| |||
Проверить, удовлетворяет ли функция 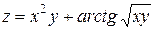 уравнение уравнение 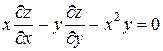
| |||
Проверить, удовлетворяет ли функция 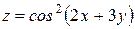 уравнение уравнение 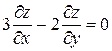
|
Найти все вторые производные функции 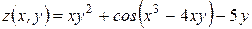
| |||
Найти все вторые производные функции 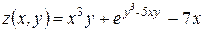
| |||
Найти все вторые производные функции 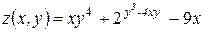
| |||
Найти все вторые производные функции 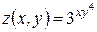
| |||
Найти все вторые производные функции 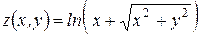
| |||
Найти все вторые производные функции 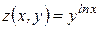
| |||
Найти все вторые производные функции 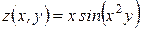
| |||
Найти все вторые производные функции 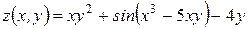
| |||
Найти все вторые производные функции 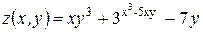
| |||
Найти все вторые производные функции 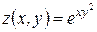
|
 2015-06-24
2015-06-24 328
328






