Интегралы по многообразию

Криволинейные интегралы первого рода Пусть в 3-х мерном пр-ве R³ задана кривая g = {r(t); a £ t £ b}. Будем рассматривать однозначные ф-ии F = F(r(t)), определенные на точках этой кривой. Если r(t) a £ t £ b какое-либо другое представление данной кривой, т.е. t = t(t) и эта ф-ия задает отображение отрезка [a, b] на [a, b], которое осуществляет эквивалентность этих представлений, то, т.к. значение ф-ии F определяется только точкой кривой g, получаем F(r(t)) = F(r(t)).Рассмотрим ф-ию F, которая принимает различные значения в точках кривой g, соответствующих различным значениям параметра, но совпадающих как точки пр-ва. Такая точка зрения соответствует физической интерпретации кривой g как траектории движения материальной точки, а ф-ии F как некоторой силы, действующей на эту мат. точку и зависящей не только от положения точки в пр-ве, но и от момента, в котором эта точка находится в данном месте. Будем пользоваться обозначениями F = F(x, y, z), т.е. сама ф-ия F определена не на всем мн-ве R³ , а только на кривой g. Пусть нам дана спрямляемая ориентированная кривая g, т.е. задано направление, причем r(s) = { x(s), y(s), z(s) 0 £ s £ S. Это ее представление, где в качестве параметра выбрана переменная длина дуги s и пусть A = r(0), B = r(S) – начальная и конечная точки дуги кривой: g = AB. Кривая g = BA – ориентированная в другую сторону. Def: Пусть на точках кривой r(s) кривой g задана ф-ия F, тогда выражение ò_AB F(x, y, z)ds = ò₀^S F(x(s), y(s), z(s))ds (1) наз-ся криволинейным интегралом 1-го рода от ф-ии F по кривой AB. Обозначается ò_AB F(r(s))ds или ò _g Fds Замечание: Хотя определение криволинейного интеграла 1-го рода связано с понятием кривой, т.е. с некоторым геометрическим образом, сам интеграл сводится к обычному интегралу по отрезку и поэтому все св-ва определенного интеграла переносятся на криволинейный интеграл 1-го рода. Специальные св-ва криволинейного интеграла 1-го рода: 1⁰ ò_AB ds = S 2⁰ Если ф-ия F непрерывна в точке кривой g как ф-ия параметра s, т.е. F(r(s)), 0 £ s £ S то ò _g Fds существует Док-во: по (1) равно интегралу по отрезку, а интеграл по отрезку непрерывен и существует 3⁰ Криволинейный интеграл 1-го рода не зависит от ориентации кривой ò_AB F(x, y, z)ds = ò_BA F(x, y, z)ds Док-во: Пусть дана т. M = r(s)ÎAB и S – длина дуги AB, тогда s – длина дуги AM. Введем параметр s = S - s, то s - длина дуги BM, тогда ф-ия r = r(S - s) 0 £ s £ S будет представлением дуги кривой BA и поэтому, выполнив в (1) замену переменных s = S - s ds = -ds: ò_ABF(x, y, z)ds =ò₀^SF(x(s),y(s),z(s))ds = -ò_S⁰F(x(S - s),y(S - s),z(S - s))ds = = ò₀^S F(x(S - s),y(S - s),z(S - s))ds ds = ò_BA F(x, y, z)ds. Это св-во криволинейного интеграла 1-го рода связано с тем, что по определению длина дуги кривой всегда считается больше нуля, независимо от того, от какой точки эта длина отсчитывается. 4⁰ Пусть t = {S_i} i от i₀ до i_k – разбиение отрезка [0, S]; x­_i – это точка из отрезка [S_{i -1}, S_i ], а DS_i = S_{i -1} – S_i, тогда DS_i - будет длинной дуги от точки r(S_{i -1}) до точки r(S_i) i от i₀ до i_k. Определим интегральную сумму Римана: st = å_{i =i 0}^ik F(r (x_i))DS_i, тогда lim _st®0 st = ò _g Fds (2) 5⁰ Пусть g – это гладкая кривая; r(t) = {j(t), y(t), c(t)} a £ t £ b - непрерывно дифференцируемое представление кривой g. Это значит, что (j’(t))² +(y’(t))² +(c’(t))² >0, " t Î[a, b] т.е. у кривой нет особых точек, в которых это представление было бы недействительно. Пусть F непрерывна на кривой g, т.е. F(r(t)) непрерывна на отрезке [a, b], тогда ò _g F(x, y, z)ds = ò_a^b F(j(t), y(t), c(t))·((j’(t))² +(y’(t))² +(c’(t))²)^1/2 dt (3), а т.к. g непрерывно дифференцируемая (спрямляемая), то примем длину дуги S = S(t) за параметр и выполним замену переменных, т.е. перейдем от t к S ds/dt = ((x’(t)²+ +(y’(t))² +(z’(t))²)^1/2 подставим в (3) и получаем док-во Замечание: Из (3) следует, что для данной кривой значение интеграла, стоящего в правой части (3) не зависит от выбора параметра на кривой, т.е. при любом выборе параметра этот интеграл равен интегралу, стоящему в левой части (3) Криволинейный интеграл 2-го рода Пусть r = r(t) - радиус-вектор движущейся мат. точки, а F = F(t) – это сила, действующая на эту точку,тогда естественно определить работу силы F вдоль траектории G движения мат. точки как ò _G Fdr. Если ф-ия F = (P, Q, R) – векторная ф-ия, dr = (dx, dy, dz) - векторная ф-ия,тогда ò _G Pdx + Qdy + Rdz; dx/ds = cosa; dy/ds = cosb; dz/ds = cosg; здесь t = (cosa,cosb,cosg) – единичный касательный вектор, тогда такая форма записи позволяет представить интеграл (1) в виде: ò _G (Pcosa + Qcosb + +Rcosg)ds Пусть AB - гладкая ориентированная кривая, (гладкая, т.е. дифференцируемая, без особых точек) тогда существует непрерывно дифференцируемое представление этой кривой: r(t) = {x = (j(t), y = y(t), z = c(t)} тогда A = r(a), B = r(b), a £ t £ b,тогда (j’(t))² +(y’(t))² +(c’(t))² >0 " t Î[a, b]. Пусть s = s(t) – переменная длина дуги 0 £ s £ S, S- длина AB, а соответствующий вектор t = (cosa,cosb,cosg) - единичный касательный вектор кривой AB, т.е. a = a(s), b = b(s), g = g(s) и пусть ф-ия N определена на мн-ве r(t), т.е. для всех точек кривой AB def: ò _AB F(x, y, z)dx = ò _AB F(x, y, z)cosads (3) ò _AB F(x, y, z)dy = ò _AB F(x, y, z)cosbds ò _AB F(x, y, z)dz = ò _AB F(x, y, z)cosgds (4) Интегралы (3,4) наз-ся криволинейными интегралами 2-го рода от ф-ии F по кривой AB. Свойства: 1⁰ Если ф-ия F непрерывна для кривой g, т.е. непрерывна как ф-ия F(r(t)) при a£ t £b, то интеграл (3) существует. Док-во: При сделанных предположениях о g: t = t(s), здесь t – это параметр на кривой g, s - переменная длина дуги, тогда t(s) будет непрерывно дифференцируема на отрезке [0, S] и поэтому ф-ия cosa = (dx/dt)·(dt/ds) и она тоже будет непрерывна на этом отрезке и, сл-но, в силу 2⁰ для криволинейных интегралов 1-го рода интеграл (3) существует 2⁰ Криволинейный интеграл 2-го рода меняет знак при изменении ориентации кривой, т.е. ò _AB F(x, y, z)dx = - ò _BA F(x, y, z)dx Док-во: a - это угол, образованный положительным направлением касательной к кривой AB с осью OX. a’ = 180 + a – это угол, образованный положительным направлением касательной к кривой BA с осью OX, cosa’ = - cosa. Теперь используем св-во 3⁰ для интеграла 1-го рода: ò _BA F(x, y, z)dx = ò _BA F(x, y, z)cosa’ds = = - ò _BA F(x, y, z)cosads = - ò _AB F(x, y, z)cosads = - ò _AB F(x, y, z)dx 3⁰ Если F непрерывная на кривой g ф-ия, то для интеграла (3) справедлива формула: ò _AB F(x, y, z)dx = ò_a^b F(j(t), y(t), c(t))· (j’(t)dt (5) Док-во: По определению криволинейного интеграла 2-го рода ò _AB F(x, y, z)dx = = ò _AB F(x, y, z)ds = ò₀^S F(x(s), y(s), z(s)) cosa = { Если заменить s = s(t), то cosa = dx/ds = = x’(t)/s’(t), тогда } = ò_a^b F(j(t), y(t), c(t))·(x’(t)/s’(t))·s’(t)dt = ò_a^b F(j(t), y(t), c(t))·(j’(t)dt,т.е. получим правую часть (5) Замечание: Интеграл в (5) не зависит от выбора параметра на кривой при условии, что параметр сохраняет ориентацию кривой Если для кривой, т.е. – однозначная ф-ия не только точек кривой, но и соответствующих точек пр-ва, тогда формула (5) примет вид: ò _g F(x, y, z)dx = ò_a^b F(x, y(x), z(x))dx (6) 4⁰ Криволинейный интеграл 2-го рода является пределом соответствующих интегральных сумм Док-во: аналогично доказательству для интеграла 1-го рода def Непрерывно дифференцируемой кривой без особых точек или гладкой кривой наз-ся кривая, для представления которой r(t) выполняется соотношение r’(t)¹0 tÎ[a, b] def Если кривая g – кусочно-гладкая, т.е. она представлена в виде объединения конечного числа гладких кривых g₁ ,g₂,…,g_k, а ф-ия F(x, y, z) определена на точках кривой g, то криволинейный интеграл 2-го рода: ò _g F(x, y, z)dx = å_i ^k_{= 1} ò _{g i} F(x, y, z)dx Формула Грина def Пусть простой замкнутый контур g является границей ограниченной плоской области G. Если ориентация контура выбрана таким образом, что при обходе контура g соответствующим возрастанием параметра, область G остается слева рис.1. Такой обход наз-ся обходом контура против часовой стрелки и такая ориентация наз-ся положительной, иначе, когда обход по часовой стрелке, ориентация наз-ся отрицательной. Обозначим g в рис.1 - g₊,а в рис.2 - g ^- def Плоскую область G, замыкание которой может быть представлено в виде = {(x, y): a £ x £ b, j(x) £ y £ y(x)} ` = {(x, y): c £ y £ d, a(y) £ x £ b(y)}, то такая область наз-ся элементарной областью. Теорема1 (Формула Грина): Пусть G – плоская область, и ее граница g – кусочно-гладкий контур и пусть область G разбита на конечное число элементарных областей G_i с соответствующими границами g_i – кусочно-гладкими i = 1,k, тогда в замыкании G заданы ф-ии P(x, y), Q(x, y) непрерывные на замыкании G со своими производными ¶P/¶y, ¶Q/¶x,тогда справедлива формула òò_G (¶Q/¶x - ¶P/¶y)dxdy = òg₊ P·dx + Q·dy
Док-во: Пусть область G – элементарная область и, сл-но, ее границу можно представить как объединение графиков 2-х кусочно-непрерывных дифференцируемых ф-ий j(x), y(x), j(x) £ y(x) при этом a £ x £ b и 2-х прямых x = a, x = b, а также как объединение 2-х графиков кусочно-непрерывных дифференцируемых ф-ий a(y) b(y), a(y) £ b(y), c £ y £ d и 2-х прямых y = c, y = d, тогда применяя правило сведения двойного интеграла к повторному, Теорему Ньютона-Лейбница и (6) получим

Рассмотрим отрезки BC и DA: ò_BC P(x, y)dx = ò_DA P(x, y)dx = 0 (**), равенство нулю следует из (3), т.к. на этих отрезках x = const, сл-но cosa = 0,. Вычтем из (*) - (**) òò_G ¶P/¶y dxdy = - ò_CD Pdx - ò_AB Pdx - ò_BC Pdx - ò_DA Pdx = - òg+ P(x, y)dx. Аналогично, из элементарности области G можно получить, что òò_G ¶P/¶x dxdy =.òg+ Q(x, y)dy Теперь, сложив два равенства, получаем формулу Грина. Замечание: Рассмотрим общий случай: пусть G разбито на элементарные области G_i. В силу доказанного " i = 1,k òò_Gi (¶Q/¶x - ¶P/¶y)dxdy = òg₊ P·dx + Q·dy. Сложив все эти соотношения, получим å_i^k₌₁ òò_Gi (¶Q/¶x - ¶P/¶y)dxdy = å_i^k₌₁ òg_i P·dx + Q·dy. В силу аддитивности двойного интеграла òò_G (¶Q/¶x - ¶P/¶y)dxdy = å_i^k₌₁ òò_Gi (¶Q/¶x - ¶P/¶y)dxdy а в å_i^k₌₁ òg_i P·dx + Q·dy криволинейные интегралы берутся дважды по всем внутренним частям границ g_i соответствующих областей G_i, т.е. части границ g_i, которые являются внутренними границами соседних областей G_i и,сл-но, не входят во внешнюю границу области G, им будет соответствовать дуга противоположной ориентации, тогда в силу свойств криволинейного интеграла 2-го рода сумма всех внутренних интегралов по внутренним границам будет равна нулю, сл-но, å_i^k₌₁ òg_i P·dx + Q·dy = = òg ₊ P·dx + Q·dy Пусть G - ограниченная область на плоскости R² и пусть ее граница состоит из Конечного числа простых контуров, которые будем называть граничными контурами. Если граничный контур одновременно является границей неограниченной области, лежащей в R² \`G, то будем его называть внешним контуром, а если он же одновременно является контуром ограниченной области в R<sup>2</sup> \`G, то будем называть его внутренним.

Если граница области G состоит из внешнего контура g_e и внутренних контуров g_i1 , g_i2 ,…, g_im и, если область G может быть разбита на конечное число элементарных относительно обеих координатных осей областей с кусочно-гладкими границами, то справедлива формула òò_G (¶Q/¶x - ¶P/¶y)dxdy = òg₊ P·dx + Q·dy + å_l^m₌₁ òg_il P·dx + Q·dy где ф-ии P и Q полагаются непрерывными вместе со своими производными в области G, а все контуры ориентированы положительно def Пусть граница ¶G ограниченной плоской области G состоит из конечного числа простых кусочно-гладких контуров. Совокупность этих контуров, ориентированных так, что при обходе по каждому из них область G остается слева (справа) называется положительной (отрицательной) ориентацией границы области G = ¶G (- ¶G) Замечание: Теорему Грина можно распространить на более общий случай, когда граница области есть объединение некоторого конечного числа отрезков (ломаная) Св-во: Вычисление площадей с помощью криволинейных интегралов. Положив в формуле Грина Q = x, P = 0, получим, что m(G) = òò_G dxdy = òg₊xdy (1) и P = - y,Q = 0 m(G) = òò_G dxdy = - òg₊ ydx (2); ((1)+(2))/2: m(G) =1/2 òg₊xdy – ydx (3) Геометрический смысл знака якобиана отображения плоской области Пусть F – взаимно однозначное непрерывно дифференцируемое отображение плоской области GÌR²_{u v} в плоскость R² _{x y} с якобианом, всюду не равным нулю, тогда G* = F(G) тоже область (по предыдущим теоремам), а якобиан, в силу его непрерывности, будет сохранять знак на области G и пусть отображение F: x = x(u, v), y = y(u, v) Лемма (без док-ва):Если g – кусочно-гладкая кривая, лежащая в области G, то ее образ g* = F(g) будет также кусочно-гладкой кривой. Пусть ГÌG—это ограниченная область, а граница ¶Г—это простой кусочно-гладкий контур: ¶Г = g и пусть Г* = F(Г)—тоже область, а по Л.: ¶Г* = F(¶Г) = g*—тоже простой кусочно-гладкий контур. Для этих контуров применима формула Грина. Пусть u = u(t), v = v(t), a £ t £ b—это представление контура g⁺ и будем предполагать, что $ и, что они непрерывны и равны друг другу во всех точках области G, тогда по (1) m(Г*) = eò_g*x dy = { e = { } = (4)

eò_a^b x y_t' dt = eò_a^b x[ + ]dt = eò_a^b x[du + dv] = eò_a^b x du + x dv] = { применим формулу Грина } =

{ P = x; Q = x; = + x; = + x; ‑ = ‑ = J(u,v)}=

= eòò_Г(‑)du dv = eòò_ГJ(u,v)du dv Левая часть равенства m(Г*) > 0, следовательно, и правая часть >0 и т.к. J(u,v) не меняет знак, значит eŸJ(u,v) > 0, т.е. знак e и знак J будут всегда одинаковыми и сл‑но, eŸJ(u,v) = |J(u,v)| и сл‑но, знак e не зависит от выбора контура g, а определяется знаком Якобиана. Теорема: Если выполнены все предположения, то справедлива формула m(Г*) = òò_Г |J(u,v)| dudv; кроме того, если якобиан положителен, то положительный обход любого контура gÎG, где g = ¶Г, ГÌG, то положительному обходу g соответствует при отображении F положительный обход контура g* = F(g), а если J(u,v) < 0 на Г, то e = ‑1 и положительному обходу всякого контура g при отображении F соответствует отрицательный обход контура g*. Вывод: Геометрический смысл знака Якобиана состоит в том, что в случае положительного Якобиана ориентация контура при отображении контура сохраняется, а отрицательного—сменяется Условие независимости криволинейного интеграла от пути интегрирования Пусть дана область G и на ней определены непрерывные функции P(x,y), Q(x,y). Рассмотрим при выполнении каких условий ò_AB Pdx+Qdy при произвольных фиксированных точках A,BÎG не зависит от выбора кривой AB, соединяющей эти точки и ÎG. Все кривые предполагаются кусочно‑гладкими, любые т. можно ломанной линией. Лемма: Условие независимости данного криволинейного ò от пути интегрирования равносильно равенству нулю интеграла по любому замкнутому контуру, лежащему в области G. Д‑во: Þ Пусть " замкнутого контура gÎG верно ò_AB Pdx+Qdy = 0 Пусть даны две кривые (AB)₁ и (AB)₂, соединяющие т. A и B. Обозначим через (BA)₂ кривую ориентированную противоположно к (AB)₂, тогда (BA)₂È(AB)₁—есть замкнутый контур и поэтому (6) Pdx+Qdy = 0. С другой стороны (6) = Pdx+Qdy + Pdx+Qdy =

(7) = Pdx+Qdy + Pdx+Qdy = Pdx+Qdy ‑ Pdx+Qdy = 0,

т.е. ò_(AB)2(Pdx+Qdy) = ò_(AB)1 (Pdx+Qdy), т.е. криволинейный интеграл не зависит от пути интегрирования, соединяющего т. A,BÎG) Ü Пусть наш интеграл òg Pdx+Qdy не зависит от пути интегрирования и пусть gÎG—замкнутый контур. Выберем на g две не совпадающие две точки A и B, тогда верно, что g = ABÈBA, тогда òg Pdx+Qdy = ò_AB Pdx+Qdy + ò_BA Pdx+Qdy = {контур ориентированный противоположно BA обозначим (AB)₁} = ò_AB Pdx+Qdy ‑ ò_(AB)1 Pdx+Qdy = {т.к. интеграл не зависит от пути интегрирования} = 0. Теорема: Пусть ф‑ции P(x,y), Q(x,y) непрерывны в плоской области G. Для того, чтобы ò_AB Pdx+Qdy при фиксированных точках A,BÎG не зависел от пути интегрирования ABÌG Û чтобы выражение Pdx+Qdy было полным дифференциалом du = Pdx+Qdy (8)

P =; Q =.

При выполнении этого условия для двух точек A(x₀,y₀), B(x₁,y₁) и для любой кривой ABÌG будет выполнятся ò_AB Pdx+Qdy = u(x₁,y₁) ‑ u(x₀,y₀) (9) Д‑во: Þ Пусть криволинейный ò не зависит от пути интегрирования и пусть дана некоторая т. M₀(x₀,y₀)ÎG и т. M(x, y), т.е. M₀M—кусочно‑гладкая кривая. Пусть u(M) = u(x, y) =_def Pdx+Qdy. Ф‑ция u(x, y) однозначна т.к. значение u(M) не зависит от выбора кривой M₀M; Покажем, что = P, = Q.

Зафиксируем т. M(x, y) и выберем т. M_h, где M_h(x+h,y). Эту точку выберем так, чтобы она ÎG. Это можно сделать всегда сделать при малом h. Рассмотрим разность u(x+h,y) - u(x, y) = Pdx+Qdy ‑ Pdx+Qdy = Pdx+Qdy = {у него y = const, следовательно dy = 0 и Qdy = 0} = Pdx = ò_x^x+hP(t)dt =

= {теперь по теореме о среднем получим} = P(x+qh, y)h, qÎ[0,1].

= p(x+qh, y) (10). Правая часть (10) в силу непрерывности ф‑ции P имеет предел, сл‑но, имеет предел и левая часть: = P(x, y) при h®0, аналогично = Q. Существование ф‑ции u, для которой верно (g), доказано.

Пусть теперь A,BÎG, ABÌG и её параметрическое представление задано в виде x = x(t), y = y(t) a £ t £ b, тогда A(x(a), y(a)), B(x(b), y(b)), тогда

ò_AB Pdx+Qdy = ò_a^b{P(x(t), y(t))x_t' + Q(x(t), y(t))y_t'}dt = ò_a^b [Ÿ + Ÿ]dt =

= ò_a^bŸdt = ò_a^bdu = u(x(b), y(b)) ‑ u(x(a), y(a)) = u(B) – u(A)—это док‑во формулы (9)

Ü Док‑во достаточности (8) непосредственно следует из независимости криволинейного интеграла от пути. Т.е. начальная точка контура замкнутого g, и по (9):

ò_gPdx+Qdy = u(A) – u(B) = 0. Def. Плоская область G наз. односвязной, если каким бы не был простой контур gÌG, где g = ¶Г, ГÌG, то эта область всегда содержится в G. Односв. область не имеет внутри дырок Теорема (без док‑ва):Пусть ф‑ции P(x, y) и Q(x, y) непрерывны вместе со своими частными производными и в плоской области G. Для того, чтобы ò_AB Pdx+Qdy при произвольных фиксированных точках A,BÎG не зависел от пути интегрирования ABÌG необходимо, а если область G односвязная, то и достаточно, чтобы во всех точках области G выполнялось =.

è Пусть криволинейный интеграл не зависит от пути интегрирования. Тогда по предыдущей теореме найдется такая функция 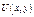, что 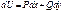. Следовательно, 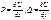. А значит 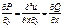. Т.к. 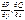непрерывны по условию, а значит непрерывны и не зависят от порядка интегрирования их вторые производные.

ç Пусть 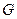- односвязная плоская область, для всех точек которой выполняется 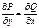. Если 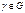- простой замкнутый кусочно-гладкий контур. А 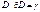(т.е. контур 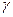), то для этой области 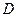применима формула Грина:

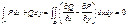Замечание: Условие = наз. критерием полного дифференциала в односвязной области. Элементы теории поверхности Пусть в пространстве R³ фиксирована декартова система координат (x, y, z). Обозначим декартовы координаты отображаемой плоскости D—u;v; рассматриваемые отображения f, r или r, —замыкание области D, ¶D—граница области D. Образ некоторой точки M обозначим f(M) = f(u, v). Def Непрерывной поверхностью S наз. всякое множество точек трёхмерного пространства R³, заданные как непрерывный образ некоторой замкнутой плоской области. Непрерывное отображение (u,v) замкнутой области на множество S наз. представлением поверхности или параметрическим представлением и обозначается S = {(u,v): (u,v)Î} (*). Переменные u,v наз. координатами или параметрами непрерывной поверхности S. Def Для непрерывной поверхности S в виде (*) множество точек пространства R³, заданное как образ границы области D при отображении r наз. краем поверхности S и обозначается ¶S = {r(u,v): (u,v)ζD} (**). Через r(u,v) обозначаем обрат т. из. Def Точка непрерывной поверхности S, в которой при данном отображении rотображается по крайней мере две точки из наз‑ся кратной точкой или точкой самопересечения. Координатная форма: r(u,v) = {x(u,v), y(u,v), z(u,v)}, либо (u,v)—это вектор, конец в точке r(u,v)ÎR³. Def Непрерывно дифференцируемой поверхностью наз. мн‑во S пр‑ва R³, заданное как непрерывно диф‑мый образ нек. замкнутой плоской области. Касательная плоскость и нормаль к поверхности Пусть задано мн‑во S = {r(u,v), (u,v)Î}. Будем считать, что пересечение каждой прямой u = u₀ или v = v₀ с замкнутой областью D состоит из одной одного отрезка (этот отрезок может вырождаться в точку) или пусто. Пусть это пересечение не пусто, тогда при фиксиров. u₀ отображение (u,v) будет некоторой непрерывно-дифференцируемой кривой, которая наз. координатной линией или u‑линией. В‑р _u' = = (x_u', y_u', z_u') является касательным вектором для нашей кривой. Аналогично _v' = = (x_v', y_v', z_v'). Def Точка r(u,v) пов‑ти S для которой векторы _u и _v не колинеарны наз. не особой точкой этой пов‑ти. Точка не особая, если [_u, _v] = _u´_v ¹ 0. Пусть u = u(t), v = v(t), 0 £ t £ b, тогда отображение (u,v) = (u(t), v(t)), при этом (u')² + (v')² ¹ 0, u’² + v’² > 0 "tÎ[a,b]. Определим понятие дифференциала для: d = _udu + _vdv; du = u'(t)dt dv = v'(t)dt Def Пл‑ть, проход‑ая через не особую точку r(u₀,v₀) пов‑ти S, в которой (пл‑ти) лежат все касательные к кривым (u(t), v(t)), проходящим через данную точку наз. касат. пл‑тью к пов‑ти в данной точке.

Если отображение = (x, y, z), ₀ = (x₀,y₀,z₀), _u = (x_u, y_u, z_u), _v = (x_v, y_v, z_v), тогда ур‑е касат. пл‑ти будет иметь вид

|| = 0; Если пов‑ть задана явно, т.е. z = f(x, y), (x, y)Î, то u = x, v = y и ур‑ие касат. пл‑ти имеет вид || = 0. Def Прямая, проход‑я через точку касания пл‑тью и перпендикулярная этой плоскости наз. нормальной к пов‑ти. Ур‑е нормальной имеет вид:

= =

Def Всякий ненулевой в‑р коллинеарный нормальной прямой, проходящей через замкнутую т. пов‑ти наз. нормалью к этой пов‑ти. Def Пов‑ть, у которой нет особых точек наз. гладкой. Первая квадратичная форма поверхности Пусть (u,v)—векторное представление пов‑ти; d = _udu + _vdv; |d|² = |_udu + _vdv|² = _u²du² + 2_vududv + _v²dv², где _vu = [_vu]. (1) Обозначим E = _u²; F = _vu; G = _v², (2) тогда |d|² = Edu² + 2Fdudv + Gdv². (2) наз. первой квадратичной формой пов‑ти. При переходе к другому базису, если базисные векторы преобразовываются с помощью матрицы перехода T = [], где u_? = j(u,v), v_? = y(u,v),

(u,v) = r(j(u,v), y(u,v)), тогда J(u,v) = []—матрица Якоби. Т.е. координаты базисных векторов преобразуются с помощью T^т = J(u,v), пусть A = []—матрица первой квадратичной формы, а A₁ = []—в новом базисе, тогда A = J^тA₁J и определитель |A| = |A₁||J|². EG‑F² = (E₁G₁‑F₁²)|J(u,v)|² (3) Кривые на поверхности Рассмотрим непрерывно-дифференцируемую кривую, лежащую на пов‑ти S; предположим, что отсчёт длины дуги L(t) производится в направлении возрастания параметра t, т.е. > 0 и = ||—свойство дуги, сл‑но, dL = |d| и dL² = |d|² = Edu² + 2Fdudv + Gdv²;

=, тогда длина дуги: L = ò_a^bdt Площадь поверхности Пусть дано непрерывно-дифференцируемое отображение (u,v), задающие гладкую пов‑ть S—это отображение определено на замкнутой области. Рассмотрим разбиение области (u,v) на квадраты ранга k, тогда замкн. обл‑ть D будет покрыта нек. конечным числом этих квадратов. Пронумеруем все не пустые пересечения этих квадратов с замкнутой обл‑тью D и обозначим все эти квадраты E_i, тогда разбиение t = {E_i: E_i = QÇ ¹ Æ, QÎT_k}, T_k—все разбиения плоскости. Рассмотрим мн‑ва E_i, которые представляют собой полностью замкнутые квадраты, лежащие в обл‑ти; эту совокупность обозначим t(¶D). Рассмотрим квадрат E_iÎt(¶D); пусть длина стороны h и пусть P_i—одна из его вершин, тогда при переходе от вершины к P_i к соседним вершинам радиус‑вектор (u,v) с точночтью до бесконечно малой порядка o(h) получим приращение |_uh|, |_vh|. Это следует из разложений (u+h,v) – r(u,v) = _uh + o(h); (u,v+h) – r(u,v) = _vh + o(h). При определении площади поверхности будем образы квадратов E_iÎt(¶D) заменять параллелограммами, построенными на векторах _uh, _vh. Обозначим площадь пов‑ти параллелограмма

Ds_i = |_uh ´ _vh |_Pi = |_u ´_v|_Pi Ÿh^2­ =

= |_u ´_v|_Pi Ÿm(E_i). Ф‑ии _u и _v непрерывны в замкнутой обл‑ти, тогда (4) limå_EiÎt(¶D)Ds_i = òò_D |_u ´_v|dudv. Def Предел (4) наз. площадью или мерой пов‑ти S: (4) = m(S) (5) т.е. m(S) = òò_D |_u ´_v|dudv. Теперь определим |_u ´_v|² =_u² _v² – (_u,_v) ² = EG – F², тогда (6) m(S) = òò_D dudv. Обозначим в (6) dudv = dS—эл‑т площади, тогда в новой системе координат m(S₁) = òò_DŸ|J(u,v)|Ÿdu₁dv₁ = {т.к. одна пов‑ть D₁} = òò_D dudv = m(S). Ориентация гладкой поверхности —правая система координат. Будем считать, что в пр‑ве R³ всегда выбирается правая система координат. Пусть S—это гладкая пов‑ть и векторное представление этой пов‑ти (u,v), причём (u,v)Î и само это представление непрерывно дифференцируемо; _u´_v ¹ 0 в области, сл‑но в каждой точке пов‑ти S можно опр‑ть нормальный единичный вектор n = (1). Def Всякая непрерывная единичная нормаль n = n(u,v), где (u,v)Î, построенная для гладкой пов‑ти S наз. ориентацией пов‑ти S. Замечание: Если n—это заданная ориентация S, то и (‑n) будет ориентацией, только отрицательной. Замечание: При регулярном преобразовании параметров u, v у пов‑ти сохраняется ориентация, если J(u,v) > 0. Def Пов‑ть, у которой фиксирована одна из её ориентаций наз. ориентированной. Def Пов‑ть S, склеенная из гладких пов‑тей S₁, S₂, …, S_m наз. кусочно‑гладкой пов‑тью. Def Пов‑ть S, склеенная из пов‑тей S₁, S₂, …, S_m наз. ориентированной, если $ такие ориентации ¶S₁, ¶S₂, …, ¶S_m краёв пов‑тей S₁, S₂, …, S_m, что для любых двух соседних пов‑тей S_i, S_j их ориентации ¶S_i, ¶S_j согласованы. Ориентации пов‑тей ¶S_i, ¶S_j наз. согласованными, если каждая из них порождает на склеивающих кривых g₁, g₂, … противоположные ориентации. Поверхностные интегралы Пусть нам дана пов‑ть S = {(u,v); (u,v)Î}, причём (1) (u,v) = {x(u,v),y(u,v),z(u,v)} и пусть представление (1)—это непрерывно‑дифференцируемое представление без особых точек; D—квадрируемая плоская область, и пусть E, G, F—коэф‑ты первой квадратичной формы и пусть на пов‑ти S задана нек. ф‑ия

Ф((u,v)) = Ф(x(u,v),y(u,v),z(u,v)) = Ф(x,y,z). (2) Def òò_SФ(x,y,z)dS = òò_DФ(x(u,v),y(u,v),z(u,v))ŸŸdudv наз. поверхностным интегралом первого рода. Если задана нек. замена переменных

(3) (2) = òò_DФ(j(u₁,v₁),y(u₁,v₁),c(u₁,v₁))Ÿ Ÿdu₁dv₁, —играет роль якобиана.
Пусть i,j,k—единичные координатные векторы, тогда нормаль

= _u´_v = || = {раскрыть по первой строке} = i + j + k (4). Если = и пусть нормаль n непрерывно продолжаема на границу обл‑ти D. Пов‑ть S, у которой выбрана ориентация n, обозначим S⁺, а для S: (‑n) обозначим S^‑. Def Поверхностные интегралы вида Ф(x,y,z)dxdy; Ф(x,y,z)dxdy (5) наз. поверхностными интегралами второго вида и определяется след. Образом

Ф(x,y,z)dxdy = òò_SФ(x,y,z)cos(^)dS (6). Ф(x,y,z)dxdy = òò_SФ(x,y,z)cos(‑n^k)dS (7). Сумма углов (n^k)+(‑n^k) =, сл‑но, cos(‑n^k) = ‑cos(n^k) и из (7) следует, что (6) = ‑Ф(x,y,z)dxdy,

т.е. ‑Ф(x,y,z)dxdy = Ф(x,y,z)dxdy (8).

Определим cos(n,k) = = = =, тогда Ф(x,y,z)dxdy = òò_SФ(x,y,z)cos(n,k)dS =

= òò_DФ(x(u,v),y(u,v),z(u,v))ŸŸŸdudv =

= òò_DФ(x(u,v),y(u,v),z(u,v))ŸŸdudv.

Аналогично

Ф(x,y,z)dydz = òò_SФ(x,y,z)cos(n^i)dS = (*)

(9) Ф(x,y,z)dzdx = òò_SФ(x,y,z)cos(n^j)dS =

= òò_DФ(x,y,z)ŸŸdudv

(10) (*) = òò_DФ(x,y,z)ŸŸdudv Замечание: Если ф‑ия z задана явно, т.е. S определяется явно заданной пов‑тью z = f(x,y), (x,y)Î, тогда интеграл первого рода òò_SФ(x,y,z)dS = òò_DФ(x,y,f(x,y))Ÿ dxdy, а ф‑лы (8), (9), т.е. интеграл второго рода: Ф(x,y,z)dxdy = òò_DФ(x,y,f(x,y))dxdy; Ф(x,y,z)dxdy = ‑òò_DФ(x,y,f(x,y))dxdy;