Определение линейного оператора и его
Пусть 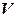 и
и 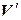 – линейные пространства над одним и тем же полем
– линейные пространства над одним и тем же полем 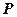 . Отображение
. Отображение 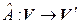 называется линейным оператором, если оно удовлетворяет следующим условиям:
называется линейным оператором, если оно удовлетворяет следующим условиям:
1. 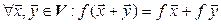 (условие аддитивности).
(условие аддитивности).
2. 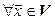
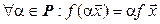 (условие однородности).
(условие однородности).
Линейный оператор также еще называют линейным отображением. Если пространства 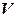 и
и 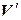 совпадают, то мы говорим «линейный оператор
совпадают, то мы говорим «линейный оператор 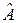 пространства
пространства 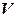 в себя» или «линейное преобразование».
в себя» или «линейное преобразование».
Очевидно, линейными являются нулевой оператор 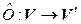 , который каждому вектору пространства
, который каждому вектору пространства 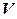 ставит в соответствие нейтральный элемент пространства
ставит в соответствие нейтральный элемент пространства 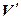 , а также тождественный оператор
, а также тождественный оператор 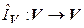 . Примерами линейных операторов также являются оператор поворота плоскости вокруг неподвижной точки
. Примерами линейных операторов также являются оператор поворота плоскости вокруг неподвижной точки 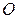 на угол
на угол 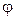 и оператор дифференцирования
и оператор дифференцирования 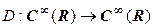 , ставящий в соответствие каждой функции ее производную (т.е.
, ставящий в соответствие каждой функции ее производную (т.е. 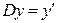 ).
).
Пример 15.3. Пусть 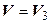 – пространство свободных векторов,
– пространство свободных векторов, 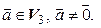 . Показать, что следующие отображения являются линейными операторами пространства
. Показать, что следующие отображения являются линейными операторами пространства 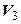 в себя: а) оператор, ставящий в соответствие каждому вектору его ортогональную проекцию на ось, направление которой задано ненулевым вектором
в себя: а) оператор, ставящий в соответствие каждому вектору его ортогональную проекцию на ось, направление которой задано ненулевым вектором 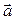 . Этот оператор в дальнейшем будем обозначать
. Этот оператор в дальнейшем будем обозначать 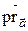 (т.е.
(т.е. 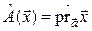 ); б)
); б) 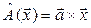 , где
, где 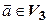 – некоторый фиксированный вектор.
– некоторый фиксированный вектор.
∆Самой сложной операцией для студентов оказывается запись образа суммы векторов. Чтобы прояснить ситуацию, представьте себе, что вам задана функция 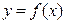 . Как вы будете искать
. Как вы будете искать 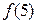 ? Конечно, вы скажете, вместо
? Конечно, вы скажете, вместо 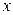 надо подставить 5. Точно так же, для нахождения
надо подставить 5. Точно так же, для нахождения 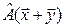 в формулу
в формулу 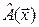 вместо
вместо 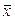 следует подставить
следует подставить 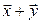 .
.
а) В аналитической геометрии доказывалось, что 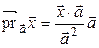 . Тогда:
. Тогда: 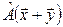 =
= 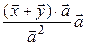 =
= 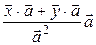 =
= 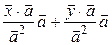 =
= 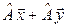 ;
;
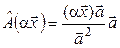 =
= 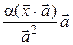 =
= 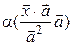 =
= 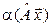
(использовались свойства скалярного произведения и произведения вектора на число). Таким образом, 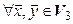 и
и 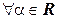 условия 1 и 2 из определения линейного оператора выполняются, а значит, оператор проектирования вектора на ось является линейным.
условия 1 и 2 из определения линейного оператора выполняются, а значит, оператор проектирования вектора на ось является линейным.
б) Для произвольных векторов 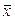 и
и 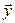 , а также для всех чисел
, а также для всех чисел 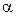 :
:
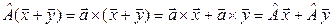 ;
; 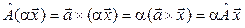 .
.
(используются свойства векторного произведения). ▲
Пример 15.4. Обозначим 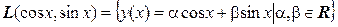 линейную оболочку функций
линейную оболочку функций 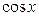 и
и 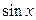 ,
, 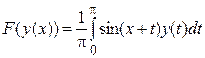 . Доказать, что отображение
. Доказать, что отображение 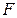 является линейным оператором пространства
является линейным оператором пространства 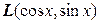 в себя.
в себя.
∆Покажем сначала, что при отображении 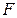 образ любой функции из пространства
образ любой функции из пространства 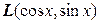 также принадлежит этому пространству. Действительно, при любых действительных
также принадлежит этому пространству. Действительно, при любых действительных 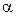 и
и 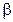 имеем:
имеем:
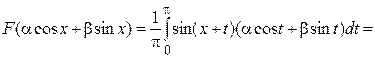
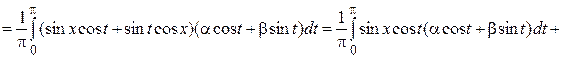
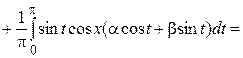
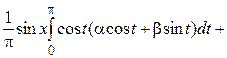
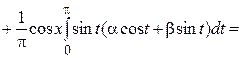
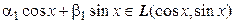 ,
,
(здесь 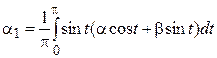 ,
, 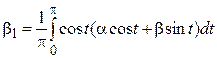 ).
).
Теперь проверим выполнение условий линейности: 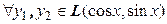 имеем:
имеем:
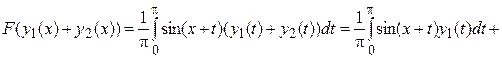
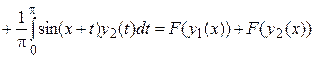 ;
;
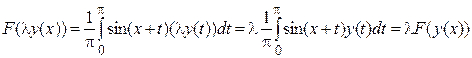 .
.
Во всех преобразованиях использовали известные свойства определенного интеграла: интеграл от суммы функций равен сумме интегралов от этих функций, а также то, что множитель, не зависящий от переменной интегрирования, можно выносить за знак интеграла. ▲
Простейшие свойства линейного оператора. 1. При линейном операторе образ линейной комбинации векторов равен такой же линейной комбинации их образов, т. е., если 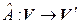 – линейный оператор, то
– линейный оператор, то 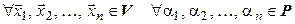 :
:
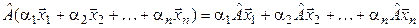 .
.
2. Линейный оператор 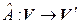 переводит нейтральный элемент пространства
переводит нейтральный элемент пространства 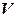 в нейтральный элемент пространства
в нейтральный элемент пространства 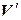 .
.
3. При линейном операторе линейно зависимые векторы пространства 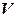 переходят в линейно зависимые векторы пространства
переходят в линейно зависимые векторы пространства 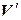 , причем сохраняются коэффициенты линейной зависимости.
, причем сохраняются коэффициенты линейной зависимости.
Теорема 15.1. Пусть 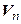 и
и 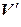 – линейные пространства над одним и тем же полем P и пусть в пространстве
– линейные пространства над одним и тем же полем P и пусть в пространстве 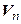 задан базис
задан базис
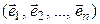 , (15.1)
, (15.1)
а в пространстве 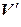 – произвольная система векторов
– произвольная система векторов
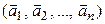 . (15.2)
. (15.2)
Тогда существует единственный линейный оператор 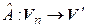 , переводящий базис (15.1) в систему (15.2), то есть такой, что
, переводящий базис (15.1) в систему (15.2), то есть такой, что 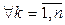 :
: 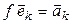 .
.
Пример 15.5. Доказать или опровергнуть утверждение: при линейном операторе линейно независимые векторы переходят в линейно независимые.
∆ Прежде чем делать какой-то общий вывод, всегда полезно посмотреть, верно ли утверждение для известных вам примеров. Так, например, при повороте плоскости на некоторый угол любые неколлинеарные векторы переходят также в неколлинеарные, т.е., действительно, линейно независимые векторы переходят в линейно независимые. А при операторе проектирования пространства, например, на ось 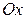 линейно независимые векторы
линейно независимые векторы 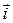 и
и 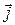 оба проектируются в
оба проектируются в 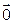 , т.е. в линейно зависимые. Таким образом, утверждение, вообще говоря, неверно. Словесный оборот «утверждение, вообще говоря, неверно» означает, что оно иногда выполняется, а иногда – нет. ▲
, т.е. в линейно зависимые. Таким образом, утверждение, вообще говоря, неверно. Словесный оборот «утверждение, вообще говоря, неверно» означает, что оно иногда выполняется, а иногда – нет. ▲
Пример 15.6. На плоскости  заданы две системы векторов:
заданы две системы векторов: 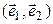 и
и 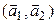 . Существует ли линейный оператор
. Существует ли линейный оператор 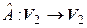 , переводящий первую систему во вторую в следующих случаях:
, переводящий первую систему во вторую в следующих случаях:
а) 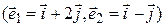 ,
, 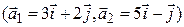 ;
;
б) 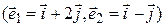 ,
, 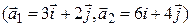 ;
;
в) 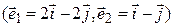 ,
, 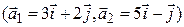 ;
;
г) 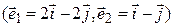 ,
, 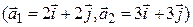 ;
;
д) 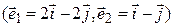 ,
, 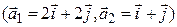 ?
?
∆ В случаях а) и б) векторы 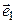 и
и 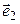 неколлинеарны, значит, образуют базис. На основании теоремы 8.1 такой оператор существует независимо от расположения векторов
неколлинеарны, значит, образуют базис. На основании теоремы 8.1 такой оператор существует независимо от расположения векторов 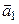 и
и 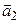 .
.
В случае в) векторы 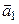 и
и 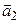 неколлинеарны, т.е. линейно независимы. Но векторы
неколлинеарны, т.е. линейно независимы. Но векторы 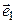 и
и 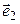 коллинеарны, т.е. линейно зависимы. На основании свойства 3 такого оператора не существует.
коллинеарны, т.е. линейно зависимы. На основании свойства 3 такого оператора не существует.
В случае г) коллинеарны обе пары векторов. На первый взгляд противоречия нет. Если же посмотреть внимательнее, заметим, что 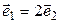 . Для любого линейного оператора
. Для любого линейного оператора 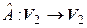 выполняется равенство
выполняется равенство 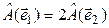 . Но
. Но 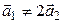 , значит, такого оператора не существует.
, значит, такого оператора не существует.
В случае д) коллинеарны обе пары векторов. Кроме того, 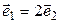 ,
, 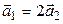 , противоречия нет. Покажем, что в этом случае линейный оператор существует. Выберем произвольный вектор
, противоречия нет. Покажем, что в этом случае линейный оператор существует. Выберем произвольный вектор 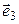 , неколлинеарный
, неколлинеарный 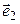 , и произвольный вектор
, и произвольный вектор 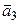 . Векторы
. Векторы 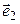 и
и 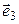 образуют базис, значит, существует линейный оператор
образуют базис, значит, существует линейный оператор 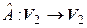 такой, что
такой, что 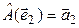 ,
, 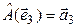 . При этом
. При этом 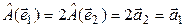 . Заметим, что в последнем случае искомый линейный оператор не только существует, но их бесконечно много. ▲
. Заметим, что в последнем случае искомый линейный оператор не только существует, но их бесконечно много. ▲
Пример 15.7. Зададим отображения трехмерного линейного пространства свободных векторов 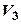 в себя следующим образом: для любого вектора
в себя следующим образом: для любого вектора 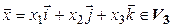 положим:
положим:
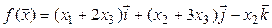 ,
, 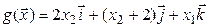 ,
, 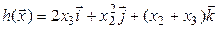 .
.
Выяснить, какие из этих отображений являются линейными.
∆ Чтобы убедиться в линейности отображения следует доказать, что условия 1 и 2 из определения линейного оператора справедливы для произвольных векторов 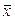 и
и 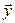 и любого числа
и любого числа 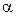 . Если же вы хотите показать, что отображение линейным не является, достаточно найти пару векторов
. Если же вы хотите показать, что отображение линейным не является, достаточно найти пару векторов 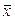 и
и 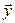 , для которых не выполняется условие аддитивности, либо вектор
, для которых не выполняется условие аддитивности, либо вектор 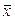 и число
и число 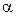 , для которых не выполняется условие однородности. Кроме того, можно показать, что не выполняется какое-либо из простейших свойств.
, для которых не выполняется условие однородности. Кроме того, можно показать, что не выполняется какое-либо из простейших свойств.
Проверим условия линейности для отображения 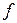 . Заметим, что во всех трех случаях координаты образа являются функциями координат прообраза. Пусть
. Заметим, что во всех трех случаях координаты образа являются функциями координат прообраза. Пусть 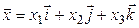 и
и 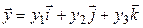 – произвольные векторы пространства
– произвольные векторы пространства 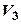 . Тогда
. Тогда 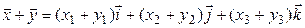 . Из условия видно: чтобы найти первую координату вектора
. Из условия видно: чтобы найти первую координату вектора 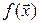 следует к его первой координате прибавить удвоенную третью. Для нахождения первой координаты вектора
следует к его первой координате прибавить удвоенную третью. Для нахождения первой координаты вектора 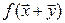 те же операции проделываем с координатами вектора
те же операции проделываем с координатами вектора 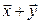 . Аналогичным образом поступаем со второй и третьей координатами, и в результате получаем:
. Аналогичным образом поступаем со второй и третьей координатами, и в результате получаем:
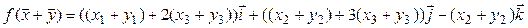 =
=
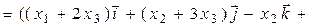
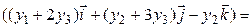
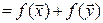 ;
;
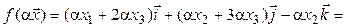
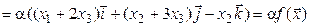 .
.
Таким образом, 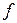 – линейный оператор.
– линейный оператор.
Рассмотрим два других отображения. Так как все координаты нулевого вектора равны нулю, то 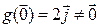 . Не выполняется второе свойство, отображение
. Не выполняется второе свойство, отображение 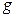 линейным не является. В записи отображения
линейным не является. В записи отображения 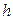 вызывает подозрение квадрат. Проверим выполнение условия однородности. Для упрощения проверки положим
вызывает подозрение квадрат. Проверим выполнение условия однородности. Для упрощения проверки положим 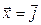 ,
, 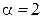 . Так как
. Так как 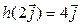 ,
, 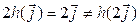 , то отображение
, то отображение  линейным не является. ▲
линейным не является. ▲
 2015-06-26
2015-06-26 4339
4339