Однотональная фазовая модуляция

При ФМ осуществляется сдвиг фазы носителя (процесса) на величину Dj(t) от средней фазы j₀. Если информация передается элементарной косинусоидальной функцией, то и фаза носителя меняется по гармоническому закону:

Dj(t) = Dj_m×cos (Wt + Ф), (4)

где:Dj_m, W, Ф – амплитуда, угловая частота и начальная фаза информационного сигнала.

Полная фаза сигнала будет определяться следующим выражением:

y(t) = j_0 + Dj_m×cos (Wt + Ф). (5)

Учитывая полученные формулы представим ФМ сигнал в следующем виде:

U_x(t) = U₀ cos [w₀t + Dj_m cos (Wt + Ф) +j₀ ]. (6)

В случае ФМ можно также воспользоваться индексом модуляции (m), учитывая, что изменение частоты в пределах ±Dw_m равносильно изменению фазы в пределах угла ±Dj_m = ±Dw_m /W. Таким образом индекс модуляции при ФМ равен девиации фазы: m = Dj_m, соответственно девиация частоты Dw_m = mW = Dj_mW. Следовательно общее выражение для ФМ можно представить в следующем виде:

U_x(t) = U₀ cos [w₀t + m cos (Wt + Ф) +j₀ ]. (7)

Различия между частотной и фазовой модуляцией проявляются при изменении частоты W модулирующего сигнала.

При фазовой модуляции девиация частоты прямо пропорциональна W, а индекс модуляции от частоты модулирующего сигнала не зависит:

m = const, ω_д = m×W.

Математическая модель однотональных ФМ (это касается и сигналов с ЧМ) сигналов с любым значением индекса модуляции m в общем случае получается разложением функции (7) в следующий ряд:

u(t)=U_m 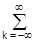J_k(N)cos[(w_o+kW)t], (8)

где J_k(N) – функция Бесселя k-го индекса от аргумента N=m. Из этого уравнения следует, что спектр сигнала содержит бесконечное число составляющих - нижних и верхних боковых колебаний, с частотами w_o±kW, которые соответствуют гармоникам частоты модуляции, и с амплитудами, пропорциональными значениям J_k(N). Амплитуды пяти первых гармоник и несущей частоты при U_m=1 в зависимости от индекса модуляции приведены на рис. 3.

При малой величине индекса модуляции m значимые амплитудные значения имеют только первые гармоники. С ростом величины m количество значимых боковых составляющих увеличивается, а энергия сигнала перераспределяется на боковые составляющие. Функции Бесселя имеют колебательный характер, поэтому спектр при удалении от несущей частоты ω_о спадает немонотонно. На рис. 3 можно также видеть, что при определенных значениях индекса модуляции (2.405, 5.52, 8.654 и т.д.) несущая частота w_o в спектре сигнала полностью отсутствует. Форма физических амплитудных спектров модулированных сигналов относительно несущей частоты при разных индексах модуляции приведена на рис. 4.

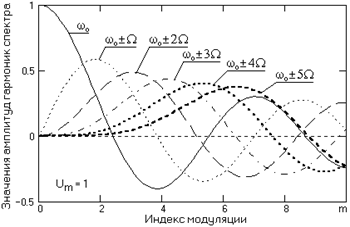
Рис. 3.

С ростом индекса модуляции полоса частот, занимаемая сигналом, расширяется. Практическая ширина спектра сигнала с угловой модуляцией определяется по формуле:

П_практ = 2(m+1)W, (9)

т.е. спектральными составляющими с номерами k>(m+1) пренебрегают. Формирование реальных сигналов, как правило, выполняется при m>>1, при этом эффективная ширина спектра равна удвоенной девиации частоты:

П_практ» 2mW = 2w_д. (10)

Рис. 4. Модули спектров ФМ сигнала при разных индексах модуляции (несущая частота 2500 Гц, гармоника модуляции 25 Гц, шкала частот в Гц относительно несущей).

Отсюда следует, что по сравнению с АМ – сигналами, полоса частот которых равна 2W, для передачи сигналов с угловой модуляцией (как с ФМ, так и с ЧМ) требуется полоса частот, в m раз большая. С другой стороны, именно широкополосность ФМ и ЧМ сигналов обеспечивает их большую помехоустойчивость по сравнению с АМ сигналами.

Для функций Бесселя имеет также место: J_-k(N) = (-1)^kJ_k(N). Это означает, что начальные фазы боковых колебаний с частотами w_o+kW и w_o-kW совпадают при четных k, и отличаются на 180^о при нечетных k.