Типовые динамические звенья

Совокупность элементарных, универсальных математических функций наиболее часто используемых при построении динамических моделей реальных объектов. Представляют собой ДУ, записанные в особой форме – в виде ПФ связывающих входной и выходной сигналы звеньев. Обычно ПФ записываются не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.

Все типовые динамические звенья 1 Безынерционное звено 2 Апериодическое звено первого порядка 3 Апериодическое звено второго порядка 4 Колебательное звено 5 Консервативное звено 6 Интегрирующее звено 7 Интегрирующее звено с замедлением 8 Изодромное звено 9 Дифференцирующее звено (с минимальным замедлением) 10 Дифференцирующее звено с замедлением

Наличие нулевых корней в числителе или знаменателе ПФ типовых звеньев – это признак для разбиения последних на три группы:

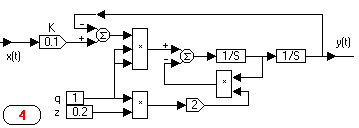
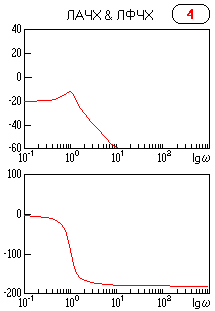
· Позиционные звенья: 1, 2, 3, 4, 5, – не имеют нулевых корней, и, следовательно, в области низких частот (т.е. в установившемся режиме), имеют коэффициент передачи равный k.

· Интегрирующие звенья: 6, 7, 8, – имеют нулевой корень-полюс, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к бесконечности.

· Дифференцирующие звенья: 9, 10 – имеют нулевой корень-ноль, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к нулю.

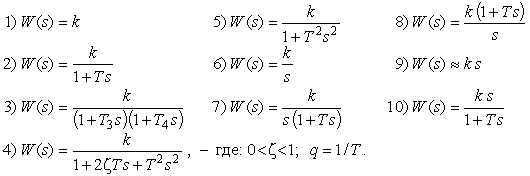
САУ может рассматриваться как некоторый преобразователь входных воздействий и начальных условий в переменные состояния и выходные переменные (величины). В случае линейного

преобразования зависимость входной х(t) и выходной у(t) описывается дифференциальным уравнением, которое с помощью оператора дифференцирования по времени р=d/dt обычно можно

записать в виде где W(p) называется передаточной функцией или операторной чувствительностью, а W0 - статической чувствительностью, т.е. чувствительностью к постоянной входной величине.

По этим уравнениям может быть составлена структурная схема системы, которая отражает (как и уравнения системы) математические преобразования над переменными. На этой

структурной схеме обычно встречаются повторяющиеся элементы, которые описывают одни и те же математические преобразования (как правило, простые: сложение, вычитание, умножение,

дифференцирование, интегрирование). Другими словами передаточная функция может быть представлена как произведение передаточных функций более простых элементов.

y=W(p)x= W1(p) W2 (p)… Wn (p)x

Такие элементы получили название динамических звеньев.

Из определений функций 1(t) и δ(t) очевидна связь между ними:

(1)

1(t)=∫δ(t) dt и δ(t)=1′(t).

Единичная ступенчатая функция 1(t) легка для практической реализации с высокой точностью, однако дельта-функцию Дирака δ(t) реализовать сложнее. Для теоретического описания систем и их моделирования ее можно грубо представить с помощью двух ступенчатых функций:

(2)

δ(t)≈ N 1(t)− N 1(t −ε),

где: N – амплитуда функций, ε – время, на которое запаздывает вторая ступенчатая функция, при этом N ε=1 и ε→0.

Переходная функция или характеристика – h (t)

Переходный процесс на выходе типового звена или линейной системы, возникающий при подаче на вход единичной ступенчатой функции 1(t).

Функция веса – w (t)

Переходный процесс на выходе типового звена или линейной системы, возникающий при подаче на вход короткого импульса, который, в приближении, можно рассматривать как дельта-функцию Диракаδ(t).

В виду независимости присущих линейным системам свойств от внешних воздействий и наличия связи (1) между последними, подобное же отношение существует и для соответствующих типовых реакций:

h (t)=∫ w (t) dt и w (t)= h ′(t).

Докажем эту взаимосвязь подав на систему грубую реализацию дельта-функции (2). В этом случае переходный процесс на выходе можно представить следующей суперпозицией:

y (t)= Nh (t)− Nh (t −ε),

которая будет являться функцией веса, предел которой (при ε→0) будет равен производной от переходной функции:

w (t)=lim_ε→₀(ε N (h (t)− h (t −ε))/ε)= h ′(t), – напомним: N ε=1.

Функция веса связана с передаточной функцией преобразованием Лапласа:

W (s)=₀^∞∫ w (t) e ⁻ ^stdt.

Переходная функция связана с передаточной функцией преобразованием Карсона:

W (s)= s ×₀^∞∫ h (t) e ⁻ ^stdt.

Для произвольного входного воздействия, переходный процесс на выходе линейной системы может быть определен на основании интеграла Дюамеля-Карсона, если известны типовые реакции:

· h (t): y (t)= x (0) h (t)+₀ ^t ∫ x ′(τ) h (t −τ) d τ;