Затем это выражение преобразуется в сумму передаточных функций с неопределенными коэффициентами

Изображение переходной функции имеет вид

.

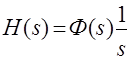Оригинал переходной функции может быть получен использованием точных и приближенных методов. Будем рассматривать только точные методы, связанные с применением обратного преобразования Лапласа.

Построение переходной функции при использовании таблиц преобразования Лапласа начинается с представления ее изображения в виде произведения передаточных функций типовых звеньев.

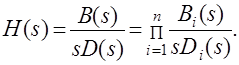
Затем это выражение преобразуется в сумму передаточных функций с неопределенными коэффициентами

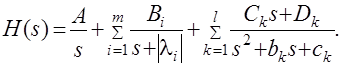(4.4)

В этом выражении A, B_i, C_k, D_k – неопределенные коэффициенты, l_i – вещественные корни уравнения D(s)=0, а выражения s²+b_ks+c_k – соответствуют комплексно – сопряженным корням характеристического уравнения. Выражение (4.4) необходимо привести к общему знаменателю и числитель полученного выражения приравнять числителю изображения исходной переходной функции B(s). Приравнивая члены при одинаковых степенях опрератора s в левой и правой частях, получим систему уравнений относительно неопределенных коэффициентов. Вычислив значения этих коэффициентов, обратимся к таблицам преобразования Лапласа и определим оригиналы слагаемых формулы (4.4). Отметим, что оригиналы, соответствующие первым двум членам суммы (4.4), определяются непосредственно из таблиц, определение оригиналов для третьего члена этой суммы могут потребоваться некоторые преобразования.

Оригинал переходной функции может быть получен использованием формулы обратного преобразования Лапласа, так называемой формулы разложения. В общем случае формула разложения имеет вид

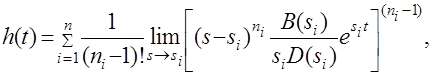(4.5)

где s_i – корни уравнения sD(s)=0, n_i- кратность корней. В случае только простых корней, когда среди них имются m вещественных корней и l пар комплексно – сопряженных корней, формула разложения принимает вид

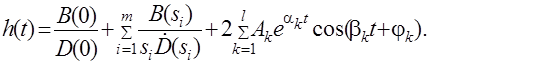(4.6)

В этом выражении a_k и b_k – вещественная и мнимая части комплексно сопряженных корней, а 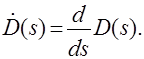Амплитуда фаза колебательных составляющих определяются следующим образом:

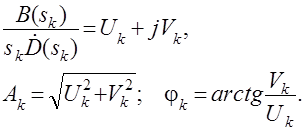
При вычислениях по этим формулам, в первую подставляется только один из пары комплексно – сопряженных корней. При вычислении фазового сдвига необходимо учитывать квадрант, в котором находиться вектор A_ke^jj_k.

Пример. Построить переходную функцию замкнутой системы управления углом тангажа и определить показатели качества.

Передаточная функция замкнутой системы имеет вид

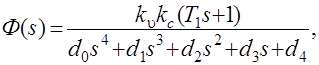
где все коэффициенты заданы или вычислены ранее. Корни характеристического уравнения равны:

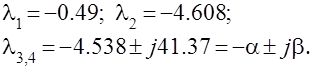
1). Построение переходной функции табличным методом.

Изображение переходной функции можно представить в виде:

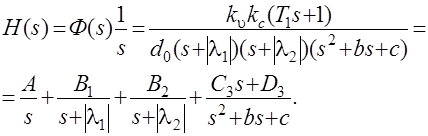
Здесь b=2a, c=a²+b².

Приведем полученное выражение к общему знаменателю и приравняем числитель этого выражения к числителю исходного изображения переходной функции. Приравняв члены при одинаковых степенях оператора s в правой и левой частях, получим систему линейных уравнений относительно неопределенных коэффициентов. Из этой системы сразу определяется А=1, после чего решается система 4-го порядка.

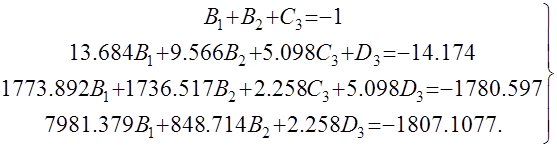
Решение этой системы дает:

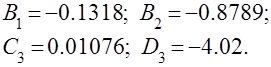
Три первых слагаемых изображения переходной функции являются твбличными. Необходимо преобразовать к табличному виду четвертое слагаемое.

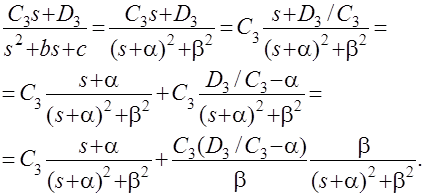
Полученные слагаемые являются табличными. Подставив численные значения параметров и использовав таблицы преобразования Лапласа, получим выражение для переходной функции 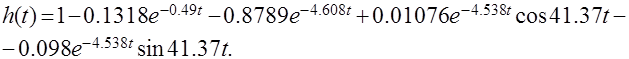2). Построение переходной функции с использованием формулы разложения.

Вначале определим составляющие процесса, соответствующие вещественным корням.

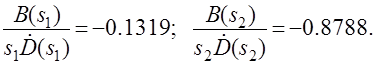
Для колебательной составляющей получим

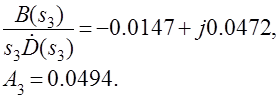
Так как вектор этой составляющей находится во втором квадранте, то

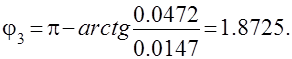
Следовательно

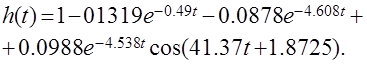
Переходные процессы, полученные различными способы совпадают с точностью до арифметических вычислений. Кривая переходной функции показана на рис.4.2. Переходный процесс практически монотонный. Колебательная составляющая фактически ни как себя не проявляет ввиду крайне малой амплитуды. Перерегулирование отсутствует: s =0. Время регулирования, определенное при D=0.05, приближенно равно 2.2 с., что для системы автоматического регулирования угла тангажа в большинстве случаев является вполне приемлемым.

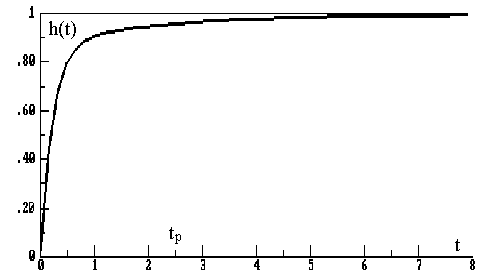
Рис.4.2. Переходная функция системы регулирования угла тангажа

4.3. Коэффициенты ошибок.

Точность САУ в установившемся режиме, при относительно медленно изменяющихся воздействиях, может быть оценена с помощью коэффициентов ошибок. Изображение ошибки определяется выражением

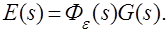
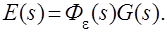
Разложим передаточную функцию системы по ошибке в степенной ряд в окрестности точки s=0. Отметим, что при s®0, t®¥ и именно поэтому мы говорим о точности в установившемся режиме.

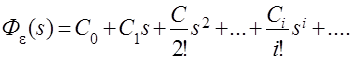(4.7)

Обозначим: 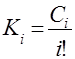и получим

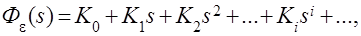(4.8)

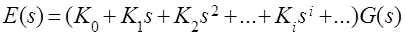
Учитывая, что оператор s, умноженный на изображение самой величины, является символом дифференцирования, можно для оригиналов записать

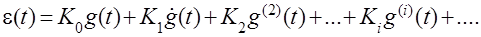(4.9)

Выражение (4.9) определяет зависимость ошибки регулирования от различных составляющих входного воздействия и коэффициенты K_i получили название коэффициентов ошибок:

- K₀ - коэффициент ошибки по положению;

- K₁- коэффициент ошибки по скорости;

- K₂ – коэффициент ошибки по ускорению и т.д.

Из (4.8) следует, что

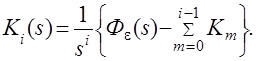
Численные значения коэффициентов ошибок определяются из этого выражения при s®0.

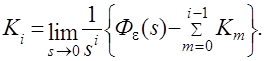(4.10)

Очевидно, что К₀=Ф_e (0).

Входное воздействие можно представить в виде степенного ряда

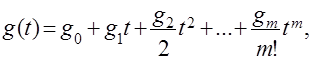
где g₀ – постоянная величина, характеризующая начальное значение, g₁=const – скорость изменения входного воздействия, g₂ = const – ускорение и т.д. Тогда

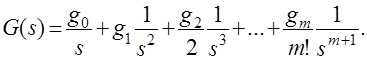
Пусть передаточная функция разомкнутой системы имеет вид

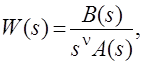
где n - порядок астатизма системы. Для передаточной функции замкнутой системы по ошибке получим

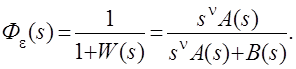
Изображение ошибки запишется в виде

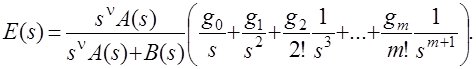
Отсюда следует, что если порядок астатизма больше порядка старшей производной воздействия, т.е. n>m, то ошибка в установившемся режиме будет равна нулю. Если n=m, то установившаяся ошибка будет равна постоянной величине, называемой статической ошибкой. И если n<m, то при t®¥ и e®¥. В отношении коэффициентов ошибок последнее выражение позволяет сделать следующие выводы.

1). Если система статическая, т.е. n=0, то существуют все составляющие ошибки и все коэффициенты ошибок не равны нулю, т.к. К₀ = Ф_e(0)¹ 0.

2).Система с астатизмом 1-го порядка, n =1, не имеет ошибки по

положению и К₀=0.

3).Система с астатизмом 2-го порядка, n =2, не имеет ошибок по положению и по скорости и К₀ =0, К₁=0.

Этот список можно продолжить. Таким образом, повышение порядка астатизма повышает точность системы в установившемся режиме. Но повышение порядка астатизма снижает запасы устойчивости, т.к. введение интегрирующих звеньев увеличивает фазовое запаздывание (снижает частоту w_p). Поэтому на практике порядок астатизма выше второго не применяют, а чаще всего ограничиваются астатизмом первого порядка, используя для повышения точности другие способы.

4.4. Интегральные оценки качества.

Интегральные оценки характеризуют качество протекания переходных процессов. Наибольшее распространение получили две интегральные оценки

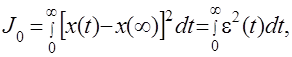(4.11)

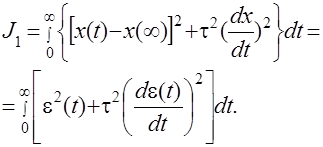(4.12)

Интеграл (4.11) определяет площадь под кривой квадрата динамической ошибки. Чем меньше этот интеграл, тем быстрее затухает переходный процесс и, следовательно, интеграл J₀ служит мерой быстродействия системы. В ряде случаев система, удовлетворяющая условию минимума J₀, имеет значительнуюколебательность переходного процесса. Для уменьшения колебательности можно попробовать воспользоваться оценкой J₁. Представим этот интеграл в виде

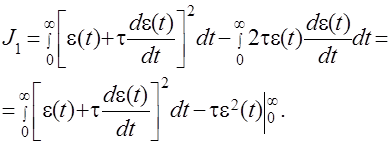
Последний член в полученном выражении является постоянной величиной и, если считать, что при t®¥ ошибка e(t)®0, то он равен te²(0). Минимальное значение интеграл J₁ будет иметь, если подинтегральное выражение будет равно нулю, т.е.

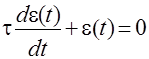(4.13)

Решение этого дифференциального уравнения будет

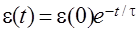(4.14)

При подаче на вход системы единичного ступенчатого воздействия начальное значение ошибки e(0)=1 и можно рекомендовать следующую методику выбора величины постоянной времени t.

1) выберем из каких – либо соображений время регулирования t_p и величину D, по уровню которой выбирается это время, т.е.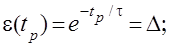

1) определим логарифм натуральный от полученного выражения

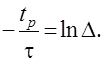
Отсюда получим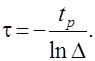

Рассмотим методику вычисления интегральных оценок при единичном ступенчатом воздействии на входе системы. Если Ф(s)=B(s)/D(s) – передаточная функция замкнутой системы, то [8,14,15]

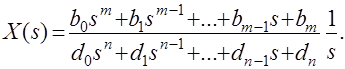
Если система устойчива, то

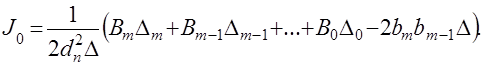(4.15)

В этом выражении: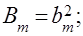

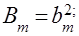
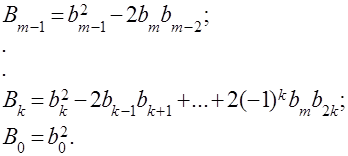
Определитель D составляется из коэффициентов характеристического уравнения замкнутой системы следующим образом

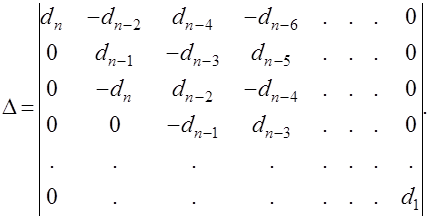
Все определители D_к (к=0,1,…m) получаются из D заменой (m+1-k) – го столбца столбцом вида (d_n-1, d_n,0,0,0,0,…0).

Интеграл J₁ можно записать в виде суммы двух интегралов

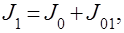
где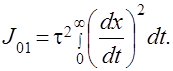

Если учесть, что 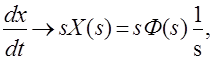то можно сделать вывод, что в новой передаточной функции порядок числителя увеличиться на единицу, т.е. m=m+1 и свободный член b_m=0. Для вычисления интеграла J₀₁ теперь можно воспользоваться выражением (4.15).

Недостатками интегральных оценок являются невозможность получения прямых показателей качества и высокая сложность вычислительных процедур. Достоинство – это возможность выразить интегральные оценки как функции параметров системы и, воспользовавшись известными методами поиска экстремума, определить значения этих параметров, дающие минимум избранной оценке. Именно это и послужило развитию аналитических методов синтеза систем автоматического управления, основанных на минимизации квадратичных интегральных оценок.