Амплитудой называется модуль наибольшего отклонения сигнала от нулевого значения. На графике амплитуде соответствует разница между самой высокой (или низкой) точкой сигнала и горизонтальной осью графика. В свою очередь, разница между самым высоким и самым низким значением называется размах сигнала.
Частота указывает на количество периодов колебаний сигнала в одну секунду и измеряется в Герцах [Гц] (1 Гц = 1 колебание в секунду). Используется также понятие круговой частоты 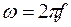 [радиан в секунду].
[радиан в секунду].
Фаза указывает на относительное временное соотношение между сигналами. Сигналы могут находиться в фазе, противофазе или некотором промежуточном положении, когда один сигнал сдвинут относительно другого.
Мощность, сигнала s(t), проходящего, например, через резистор электрической цепи, определяется по формуле 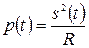 . Такая мощность называется мгновенной.
. Такая мощность называется мгновенной.
Энергия сигнала на интервале существования Т определяется по формуле 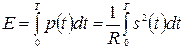 . Для сигналов с ограниченной энергией выполняется соотношение
. Для сигналов с ограниченной энергией выполняется соотношение 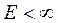 . В свою очередь, периодический гармонический сигнал имеет бесконечную энергию.
. В свою очередь, периодический гармонический сигнал имеет бесконечную энергию.
Средняя мощность сигнала на интервале времени определяется по формуле: 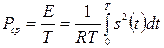 .
.
В теории обработки сигналов принято использовать эти выражения при значении R =1. Тогда: 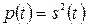 ,
, 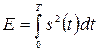 ,
, 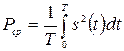 (т.к. R =1, то более строгое название – удельная мощность и удельная энергия). Если уровень сигнала измеряется в вольтах [В], то мощность здесь имеет размерность В2, а энергия – В2 с.
(т.к. R =1, то более строгое название – удельная мощность и удельная энергия). Если уровень сигнала измеряется в вольтах [В], то мощность здесь имеет размерность В2, а энергия – В2 с.
Для сигналов с бесконечной энергией, можно определить их среднюю мощность во всем времени их существования, устремив интервал усреднения в бесконечность: 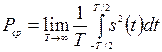 . Средняя мощность в такой трактовке представляет собой средний квадрат сигнала (MSQ – mean square).
. Средняя мощность в такой трактовке представляет собой средний квадрат сигнала (MSQ – mean square).
Действующее значение сигнала (RMS – root mean square): 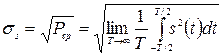 .
.
При оценке случайных сигналов используются статистические характеристики, такие как математическое ожидание (среднее), дисперсия, стандартное отклонение.
Математическое ожидание (или среднее) дискретного сигнала определяется согласно выражению: 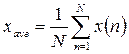 , где N - количество отсчетов.
, где N - количество отсчетов.
Дисперсия определяется согласно выражению: 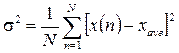 .
.
Положительный квадратный корень из дисперсии указывает на стандартное отклонение 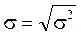 .
.
Для расчета среднего и дисперсии применяется также функция плотности вероятности, которая представляет собой меру правдоподобия появления некоторого значения сигнала. Для непрерывного сигнала значения функции плотности вероятности всегда положительные, а сумма всех ее значений равна единице. С учетом этого, математическое ожидание (среднее) случайного сигнала можно определить по выражению 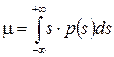 , а дисперсия -
, а дисперсия - 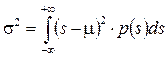 , где p(s) - функция плотности вероятности.
, где p(s) - функция плотности вероятности.
Одна из функций плотности вероятности используется наиболее часто и называется нормальной функцией плотности вероятности (рис.2).
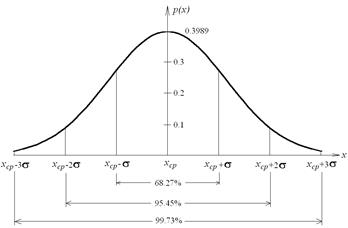 | Такая функция показывает, что 68.27% случаев значений сигнала отличаются от среднего не более чем на стандартное отклонение, 99.73% случаев значений сигнала находятся в пределах от среднего до трех стандартных отклонений. Площадь под кривой равна единице. |
| Рис.2. Нормальная функция плотности вероятности |
Таким образом, математическое ожидание показывает уровень, относительно которого располагаются отдельные отсчеты сигнала, а дисперсия является мерой отклонения значений этих отсчетов. По аналогии с детерминированными сигналами можно утверждать, что математическое ожидание – это постоянная составляющая случайного сигнала, дисперсия – мощность переменной составляющей, а стандартное отклонение – амплитуда переменной составляющей.
Статистические характеристики могут использоваться и при анализе детерминированных сигналов. Например, стандартное отклонение для синусоиды, среднее значение которой равно нулю, имеет значение:
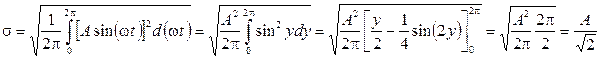 .
.
Эта характеристика, рассчитанная при нулевом среднем, называется среднеквадратическим значением. В свою очередь, дисперсия синусоиды равна 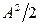 .
.
 2015-07-04
2015-07-04 6247
6247
