Определение стрелки кривой

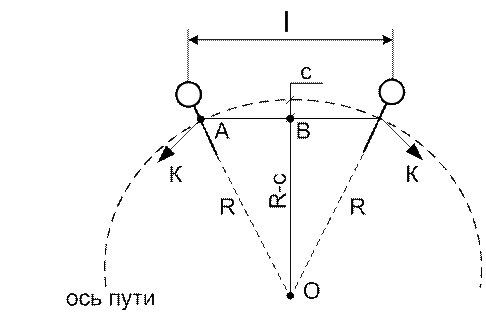
рис. 18.6

На рис.18.6 показано:

О – центр кривой;

с – стрелка кривой (расстояние контактного провода до оси пути).

По теореме Пифагора можно записать: 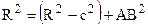, если 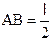, то

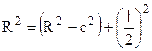
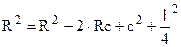
В действительности значение стрелки кривой (с) очень мало, а при возведении в квадрат стремиться к нулю, следовательно: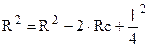

из последнего выражения выведем значение (с).

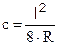
Расположим контактный провод на кривом участке пути с зигзагом.

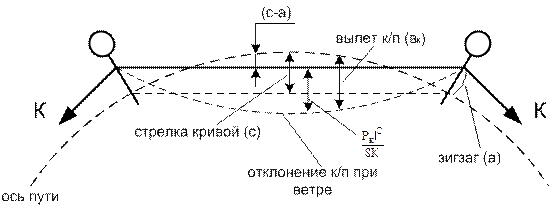
рис. 18.7

;

;

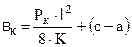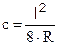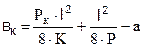
Преобразуя последние выражения относительно длины пролета, а также принимая в виду, что при 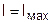; 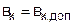получим:

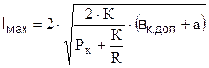
Вводим в последнее выражение 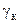имеем:

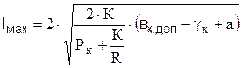
Последнее выражение – формула определения длины пролета на кривом участке пути.