2015-07-04
791Пусть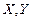 
- банаховы пространства.
Определение.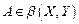 
называется вполне непрерывным, если для любого 
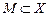ограниченный образ 
является относительным компактом в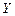 
.
Таким образом, вполне непрерывный оператор удовлетворяет двум условиям
1. является непрерывным;
2. переводит каждое ограниченное множество в относительно компактное.
Так как относительная компактность отличается от ограниченности тем, что всякая последовательность имеет сходящуюся подпоследовательность, тем самым о вполне непрерывных операторах можно говорить, что они улучшают свойства множеств.
Утверждение 1 (критерий Хаусдорфа). 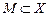является относительным компактом тогда и только тогда, когда для любого 
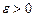существует конечная 
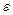сеть.
Утверждение 2. Непрерывный образ компакта является компактом. Т.е. если 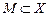- компакт, 
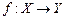- непрерывный оператор, то 
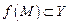- компакт.
Теорема 1. Есл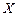и 
и 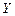- конечномерное пространство, то любой ограниченный оператор 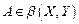является вполне непрерывным.
Теорема 2. Пусть пространства 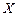и 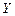бесконечномерны (
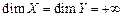) и линейный ограниченный оператор 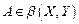обратим, т.е. существует оператор 
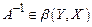. Тогда 
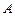не является вполне непрерывным.
|
|
|
Теорема 3. Пусть операторы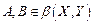 
- вполне непрерывны. Тогда оператор 
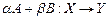- вполне непрерывный.
Теорема 4. Пусть последовательность вполне непрерывных операторов в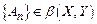 
сходится по операторной норме (т.е. 
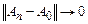при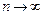 
)
,
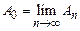тогда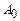 
- вполне непрерывный.
