Общие сведения

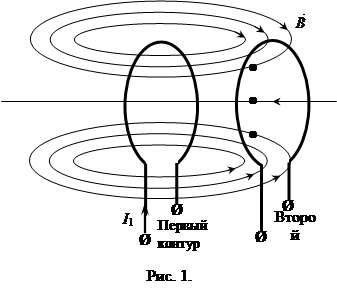
Рассмотрим два контура, изготовленных из проволоки (рис. 1).

Пусть в контуре 1 протекает электрический ток силой I ₁ ампер. Этот электрический ток вызывает магнитное поле, тем больше, чем больше сила тока I ₁ Часть силовых линий этого поля пересекает площадь второго контура. Таким образом, магнитный поток Ф _2,1, проходящий через площадь второго контура будет пропорциональна I ₁:

Ф _2,1= M _2,1 I ₁ (1)

где M _2,1 коэффициент пропорциональности.

Если источник тока отключить от первого контура и подключить ко второму, то в нём возникнет электрический ток I _2.. Теперь магнитный поток, создаваемый током I ₂ и проходящий через площадь, первого контура, будет равен Ф _1,2= M _1,2 I ₂, причем можно показать, что:

M _2,1 = M _1,2 = M.

Если контуры состоят не из одного витка, как на рисунке 1, а каждый из нескольких витков, то необходимо находить поток магнитного поля через площадь всех витков конкретного контура. Пропорциональность силе тока, вызывающей магнитное поле, и в этом случае сохраняется, но теперь поток идущий через площадь всех витков контура называется потокосцеплением и обозначается греческой буквой .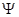

Так, например, если электрический ток идёт по виткам первого контура (сила тока I ₁), то имеем для потокосцепления, проходящего через площадь всех витков второго контура:

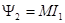(1)

Коэффициент пропорциональности М называется коэффициентом взаимной индукции и в системе СИ измеряется в Генри (Гн). Численное значение коэффициента взаимной индукции зависит от формы, размеров, числа витков в каждом из контуров, взаимного их расположения и магнитных свойств среды.

В настоящей лабораторной работе в качестве первого контура используется длинный соленоид; в качестве второго контура используется короткий соленоид малого диаметра (катушка). Соленоиды расположены соосно (рис.2). Допустим, что по виткам первого контура (длинный соленоид) идёт ток I ₁. Тогда внутри его создаётся магнитное поле с индукцией:

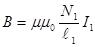(2)

где: 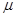– магнитная проницаемость среды, заполняющей соленоид (в нашем случае это воздух - 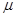=1); 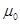– магнитная постоянная ( 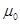=4 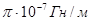); N ₁ – число витков в соленоиде; 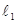– длина соленоида.

Определим теперь потокосцепление, то есть магнитный поток, проходящий через площадь всех витков второго контура (число витков равно N ₂, площадь витка S ₂)

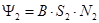
Представляя выражение для В (формула 2) получаем:

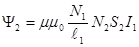(3)

Сравнивая формулы (1) и (3) получаем для коэффициента взаимной индукции соосных соленоидов:

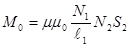(4)

Если соленоиды не сосны, а их оси составляют друг с другом угол 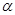, то коэффициент взаимной индукции уменьшается и будет:

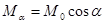(5)

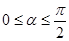
В лабораторной работе используется переменный электрический ток, который идёт по виткам длинного соленоида. В результате, внутри соленоида возникает переменное магнитное поле, которое, в соответствии с законом электромагнитной индукции Фарадея вызывает появление переменной ЭДС индукции (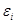) на зажимах второго контура:

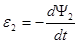
Подставляя соотношение (1) имеем:

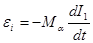(6)

Сила тока в первом контуре изменяется по закону:

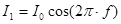
где 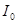– амплитуда тока (А); 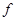– частота переменного тока (Гц). Подставив выражение для силы тока в (6) получим:

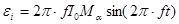
Из последней формулы следует, что амплитуда напряжения на зажимах второго контура будет равно:

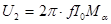
Из последней формулы ясно, что коэффициент взаимной индукции может быть определён, если измерены :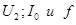

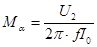(7)

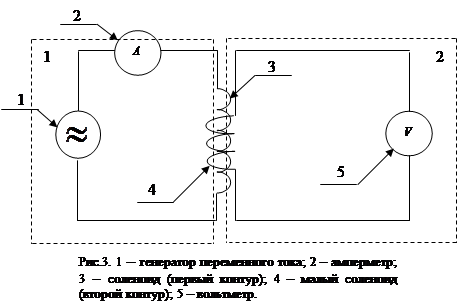Принципиальная схема установки